evinda
Gold Member
MHB
- 3,741
- 0
Hello again! (Wasntme)
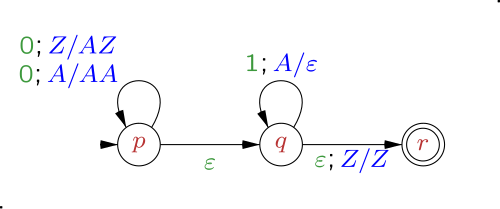
I have to show that the language \left \{ w\epsilon \left \{ a,b \right \}^{*}:w=a^{m}b^{n},m\neq n \right \} is accepted by a pushdown automaton.
Can I use the sentence "A string is accepted by a pushdown automaton if,starting with an empty stack,there is a path through the automaton such that the automaton stops in an accepting state after the entire string has been read." to show it?
I have to show that the language \left \{ w\epsilon \left \{ a,b \right \}^{*}:w=a^{m}b^{n},m\neq n \right \} is accepted by a pushdown automaton.
Can I use the sentence "A string is accepted by a pushdown automaton if,starting with an empty stack,there is a path through the automaton such that the automaton stops in an accepting state after the entire string has been read." to show it?