evinda
Gold Member
MHB
- 3,741
- 0
I like Serena said:Oh wait!
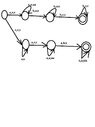
The PDA correctly accepts $a^nb^nb^+$ in the upper branch.
However, in the lower branch it accepts $b^na^na^+$... that is not right.
It should accept $a^+a^nb^n$.
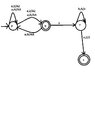
I have changed it :) Is it right now?
View attachment 1822