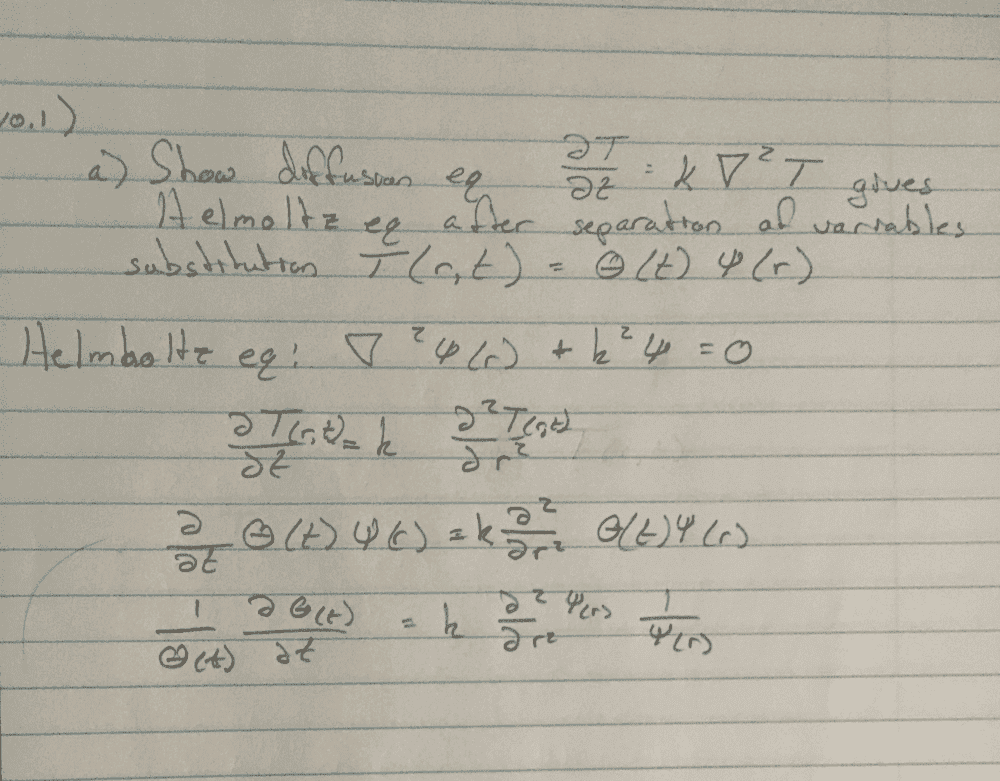SUMMARY
The discussion focuses on the mathematical manipulation required to derive the Helmholtz equation from the diffusion equation. Participants emphasize the importance of distinguishing between the constants \( k \) and \( \kappa \) and suggest that algebraic manipulation of the equation \( \kappa \frac{\nabla^2 \psi(\mathbf{r})}{\psi(\mathbf{r})} = C \) can yield the Helmholtz equation without solving for \( \psi \). Key techniques include separation of variables and proper handling of boundary conditions. The conversation highlights the necessity of understanding the dimensionality of the problem when applying the Laplacian operator.
PREREQUISITES
- Understanding of differential equations, specifically the diffusion equation and Helmholtz equation.
- Familiarity with algebraic manipulation of equations in multiple dimensions.
- Knowledge of separation of variables technique in solving partial differential equations.
- Ability to distinguish between constants in mathematical equations, such as \( k \) and \( \kappa \).
NEXT STEPS
- Study the derivation of the Helmholtz equation from the diffusion equation in detail.
- Learn about the separation of variables method for solving partial differential equations.
- Explore the implications of boundary conditions on solutions to the Helmholtz equation.
- Review the properties and applications of the Laplacian operator in different dimensions.
USEFUL FOR
Students and professionals in applied mathematics, physics, and engineering who are working with differential equations, particularly those interested in the relationship between diffusion processes and wave equations.