Show that the flywheel inside the train counteracts lean in a curve

[Karl Karlsson]

Summary: Consider a train carriage rolling along a curve that forms a left turn on the track. The carriage speed is directed along the y-axis (into the plane of the paper) in the figure. The trolley will have a tendency to curl in the curve in the specified direction. A flywheel is inserted which rotates with a large angular velocity ω0 around its axis of symmetry along the x-direction. Decide whether ω0 should be directed in the positive or negative x direction to counteract the rolling of the carriage.

Consider a train carriage rolling along a curve that forms a left turn on the track. The carriage speed is directed along the y-axis (into the plane of the paper) in the figure. The trolley will have a tendency to curl in the curve in the specified direction. A flywheel is inserted which rotates with a large angular velocity ω0 around its axis of symmetry along the x-direction. Decide whether ω0 should be directed in the positive or negative x direction to counteract the rolling of the carriage. Motivation is required.

Solution:

I understand the whole solution up to the last line. My reasoning why the vector w0 should be directed in the negative x direction:
w1 is a constant. In order to

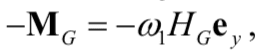something in the right must have the opposite direction compared to what it had before, this can also be seen from the cross product on line 5 in the solution. Since w1 is constant, it must be the angular momentum of the mass centra that has the opposite direction, when we calculated MG, the momentum of motion was directed along the x-axis, now it must be directed along the minus x-axis and hence the vector w0 must be directed in the negative x direction. Can anyone mathematically show why I'm wrong. Thanks!

 

[TSny]

I'm having some trouble understanding the description of your reasoning.

As the carriage makes a left turn, the flywheel changes its orientation. The vector $\mathbf M_G$ is the torque ("moment of force") that must be applied to the flywheel in order to cause the flywheel to change its orientation. This torque comes from the supports at each end of the axis of the flywheel. These supports are attached to the walls of the carriage. So, $\mathbf M_G$ is the torque that the carriage applies to the flywheel. Therefore, the flywheel applies a reaction torque of the same amount but in the opposite direction to the carriage. Thus, the flywheel exerts a torque $- \mathbf M_G$ to the carriage. You need to show that $- \mathbf M_G$ is in the direction that helps to prevent the carriage from tipping over if $\boldsymbol \omega_0$ is in the positive x direction (as shown in the figure).

Is this how you are thinking about it? If you understand the solution up to the last line, then you understand that $\mathbf M_G$ is in the positive y-direction if $\boldsymbol \omega_0$ is in the positive x-direction. (The solution is based on the assumption that $\boldsymbol \omega_0$ is in the positive x-direction. See the third line of the solution and also the figure.) Therefore, $- \mathbf M_G$ is in the negative y-direction. Is this the correct direction in order to help prevent the carriage from tipping?

 

[Karl Karlsson]

I'm having some trouble understanding the description of your reasoning.

As the carriage makes a left turn, the flywheel changes its orientation. The vector $\mathbf M_G$ is the torque ("moment of force") that must be applied to the flywheel in order to cause the flywheel to change its orientation. This torque comes from the supports at each end of the axis of the flywheel. These supports are attached to the walls of the carriage. So, $\mathbf M_G$ is the torque that the carriage applies to the flywheel. Therefore, the flywheel applies a reaction torque of the same amount but in the opposite direction to the carriage. Thus, the flywheel exerts a torque $- \mathbf M_G$ to the carriage. You need to show that $- \mathbf M_G$ is in the direction that helps to prevent the carriage from tipping over if $\boldsymbol \omega_0$ is in the positive x direction (as shown in the figure).

Is this how you are thinking about it? If you understand the solution up to the last line, then you understand that $\mathbf M_G$ is in the positive y-direction if $\boldsymbol \omega_0$ is in the positive x-direction. (The solution is based on the assumption that $\boldsymbol \omega_0$ is in the positive x-direction. See the third line of the solution and also the figure.) Therefore, $- \mathbf M_G$ is in the negative y-direction. Is this the correct direction in order to help prevent the carriage from tipping?

You seem to understand exactly my reasoning. Yes, I understand that $\mathbf M_G$ is in the positive y-direction if $\boldsymbol \omega_0$ is in the positive x-direction. The moment of force from the flywheel on the carriage must then be $- \mathbf M_G$ directed in the negative y - direction, but then $\boldsymbol \omega_0$ must be in the negative x - direction in order to prevent the carriage to tip over. Right?

 

[TSny]

You seem to understand exactly my reasoning. Yes, I understand that $\mathbf M_G$ is in the positive y-direction if $\boldsymbol \omega_0$ is in the positive x-direction. The moment of force from the flywheel on the carriage must then be $- \mathbf M_G$ directed in the negative y - direction, but then $\boldsymbol \omega_0$ must be in the negative x - direction in order to prevent the carriage to tip over. Right?

I don't understand the last part where you say, "but then $\boldsymbol \omega_0$ must be in the negative x - direction in order to prevent the carriage to tip over."

Does everything in the following two figures make sense to you?

You can see that in order for the flywheel to apply a torque in the correct direction as shown in the figure on the right, $\boldsymbol \omega_0$ must be in the positive x-direction.

 

[TSny]

Be sure that you understand how Newton's 3rd law comes into play. If the carriage exerts a force on the flywheel at one end of the axis of the flywheel, then the flywheel exerts an equal but opposite force on the carriage at that point. It's a good idea to draw the forces acting at the ends of the flywheel.