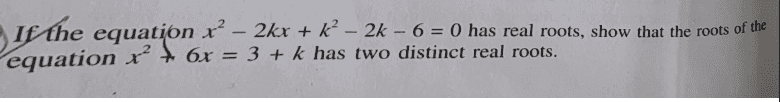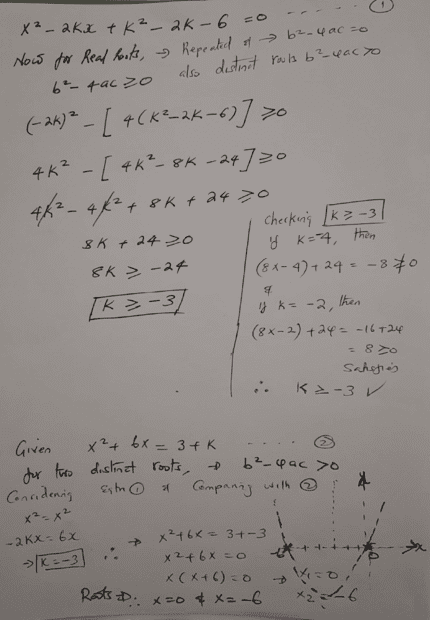Homework Help Overview
The discussion revolves around establishing conditions for a quadratic equation to have two distinct real roots, specifically focusing on the parameter \( k \) in the equations \( x^2 + 6x = 3 + k \) and another unspecified quadratic equation. Participants are exploring the implications of different values of \( k \) and how they relate to the existence of real roots.
Discussion Character
- Exploratory, Assumption checking, Mathematical reasoning
Approaches and Questions Raised
- Participants discuss the conditions under which the quadratic equations yield distinct real roots, with some suggesting that \( k \) should be considered over a range rather than a single value. There are inquiries about how to relate different conditions derived from analyzing the equations, particularly regarding \( k > -12 \) and \( k \ge -3 \).
Discussion Status
The discussion is active with various interpretations being explored. Some participants have offered insights into the conditions for \( k \) based on their analyses, while others express confusion about how these conditions interrelate. There is no explicit consensus, but multiple lines of reasoning are being examined.
Contextual Notes
Participants are navigating the implications of specific values of \( k \) and the conditions necessary for the quadratic equations to have real roots. The discussion is influenced by the original problem's requirements and the mathematical properties of quadratics.