Showing that a given propagator is proportional to Green's function

[JD_PM]

Homework Statement

Given


\begin{equation*}
\mathcal{L} = -\frac 1 4 F_{\mu \nu}F^{\mu \nu} + \frac{m^2}{2} A_{\mu}A^{\mu}
\end{equation*}

Where the strength tensor $F_{\mu \nu}$ is given by

\begin{equation*}
F_{\mu \nu} = \partial_{\nu}A_{\mu} - \partial_{\mu}A_{\nu}
\end{equation*}


The E.O.M., obtainable out of $\mathcal{L}$, is given by



\begin{equation*}
\Box A^{\mu} - \partial^{\mu} (\partial_{\nu} A^{\nu}) + m^2 A^{\mu} = 0
\end{equation*}


The Feynman propagator for this field is given by

\begin{equation*}
\langle 0 |T\{A^{\mu}(x)A^{\nu}(y)\}|0\rangle = -i \int \frac{d^4 k}{(2\pi)^4} \exp\left( -ik \cdot (x-y)\right) \frac{\eta^{\mu \nu}-k^{\mu}k^{\nu}/m^2}{k^2-m^2+i\varepsilon}
\end{equation*}


Working in momentum-space, show that the propagator is proportional to Green's function for the equation of motion. In other words, find the Green’s function of the equation of motion and use this to determine the propagator (Hint: it is not the aim to calculate Green's function using the Feynman propagator, instead we want to think of it as taking the Fourier transform of the inverse of the equation of motion).

Relevant Equations

N/A

First off let me say I am a bit confused by this question.

Searching for some references I found the following related to the KG propagator, given by (P&S, chapter 2 pages 29, 30)

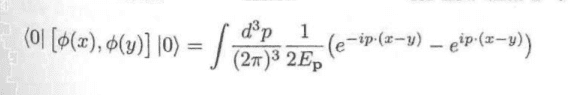
Then they Fourier-transformed the KG propagator

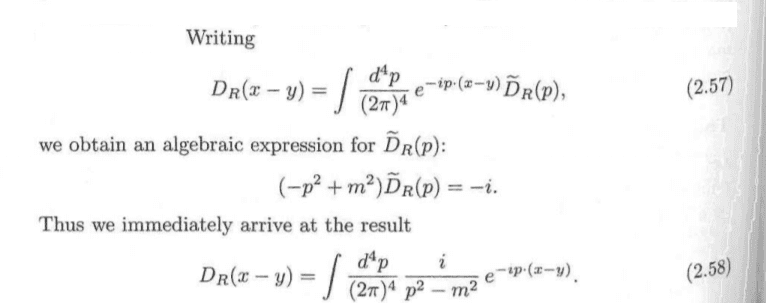
Is this what is aimed with this exercise? If yes, could you please give me a hint on how to apply the idea to the given problem?Thank you

 

[Nate810]

The KG propagator is essentially a mathematical tool for describing the propagation of a particle through space and time. It is used to calculate how a particle evolves between two points in space-time. The Fourier transform of the KG propagator is used to describe how a particle moves from one point in space-time to another in terms of momentum space. In order to apply this idea to the given problem, you would need to know the initial and final states of the particle in question (i.e. the position and momentum at each point). Then, you can use the KG propagator to calculate the evolution of the particle's state between these two points. Finally, you can perform a Fourier transform of the KG propagator to obtain a description of the particle's motion in terms of momentum space.