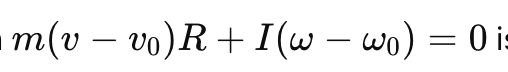mancity said:
Thank you providing it. It is informative. Note that applies to a ball that is constrained to rotate about a fixed axis o=passing through a diameter. The results from E10-8 cannot be applied to the present case without justification and expansion to the more general case of a ball whose center mass is free to move.
That said, I think that you are understandably confused and I believe that your confusion stems from a lack of understanding of the direction of the vector quantities in the scalar equation $$L=mv_0R+I\omega_0.$$ A derivation of this equation appeared as post #282
here. Because this thread has a total of 336 posts, I have pasted the derivation with minor editorial changes to spare you the trouble of sifting through everything that was said then.
Consider an irregular rigid object of mass ##M## simultaneously rotating and translating in space in the absence of external forces and torques (see figure on the right). This means that both its linear and angular momentum are conserved. We will calculate its angular momentum about an arbitrary point A (see diagram below) given that the velocity of the center of mass is ##\vec V_{cm}## and its rotational angular velocity is ##\vec \omega.##
First we point out that the axis of rotation must pass through the CM. That's because linear momentum is conserved which means that ##\vec V_{cm}= \rm{const.}## If the axis of rotation did not pass through the CM, the CM would rotate about that hypothetical axis and its velocity would change direction which means that it cannot be constant. Thus, the linear velocity relative to the CM of an arbitrary point P at position ##\vec {r}'## from the CM is ##\vec {v}'=\vec{\omega}\times \vec {r}'.##
Now consider mass element ##dm## at point P the position vector of which relative to A is ##\vec r##. Let ##\vec {r}' ## be the position vector of ##dm## relative to the CM and ##\vec R## be the position of the CM relative to A. Finally, let ##\vec v_P## be the instantaneous velocity of point P relative to point A. Addition of velocities requires that the velocity of point P relative to A is ##\vec v_P=\vec V_{cm}+\vec{\omega}\times \vec {r}'.##
The angular momentum contribution of ##dm## about point A is $$d\vec L=(dm)\vec r\times \vec v_P=(dm)(\vec R+\vec {r}')\times(\vec V_{cm}+\vec{\omega}\times \vec {r}')$$ We multiply out the cross product on the RHS and consider each of the four resulting terms separately.
1. ##~(dm) \vec R \times \vec V_{cm}##
The contribution from the first term to the total angular momentum is $$\vec L_1=\int (dm) \vec R \times \vec V_{cm}=\left( \int dm \right) \vec R \times \vec V_{cm}=M\vec R \times \vec V_{cm}.$$ I have seen this called the angular momentum of the center of mass, the translational angular momentum or the orbital angular momentum.
2. ##~(dm)\vec R\times (\vec{\omega}\times \vec {r}')##
Using the triple-product rule,
$$\vec R\times (\vec{\omega}\times \vec {r}')=\vec{\omega}(\vec R\cdot \vec {r}') -\vec {r}'(\vec R \cdot \vec{\omega}).$$The second term on the RHS is zero because ##\vec R## is perpendicular to ##\vec {\omega}##. To find the contribution of the first term, we integrate $$\vec L_2=\int (dm)\vec{\omega}(\vec R\cdot \vec {r}')=\vec{\omega}\left(\vec R\cdot \int (dm)\vec {r}'\right)=0$$ Note that by definition of the CM coordinates, ##\int (dm)\vec {r}'=0.##
3. ##~(dm)\vec {r}'\times \vec V_{cm}##
This term also vanishes upon integration for the same reason when we take constant ##\vec R## out of the integral. $$\vec L_3=\int (dm)\vec {r}'\times \vec V_{cm}=\left(\int (dm)\vec {r}'\right)\times \vec V_{cm}=0.$$ 4. ##~(dm)\vec {r}'\times (\vec{\omega}\times \vec {r}')##
Triple-product rule once more
$$\vec {r}'\times (\vec{\omega}\times \vec {r}')=\vec{\omega}(\vec {r}'\cdot \vec {r}')-\vec {r}'(\vec{\omega}\cdot \vec {r}').$$The second term on the RHS vanishes because the vectors are orthogonal. Integrating the first term, $$\vec L_4=\int \vec{\omega}(\vec {r}'\cdot \vec {r}')=\vec{\omega}\int (dm){r'}^2=I_{cm}~\vec{\omega}.$$I have seen this called the angular momentum about the center of mass or the rotational angular momentum or the spin angular momentum.
Thus, the total angular momentum about point A of the translating and rotating rigid body is the sum of four terms two of which are zero, so that $$\vec L=M\vec R \times \vec V_{cm}+I_{cm}~\vec{\omega}.\tag{1}$$ The first term in this expression, angular momentum of the center of mass, depends on the choice of reference point A. The second term, angular momentum about the center of mass, does not.
The bottom line is that one can always write the angular momentum of a simultaneously translating and rotating rigid body in the form of Equation (1).
In this equation the first term is ##\vec L_{\text{translatonal}}=M\vec R \times \vec V_{cm}## is the translational angular moment of the center of mass about point A, i.e. the angular momentum that any moving point mass has relative to a fixed point. Its direction is perpendicular to the plane defined by the position vector ##\vec r## from point A and the velocity vector ##\vec v## (right hand rule.)
The second term is the angular momentum about the center of mass, i.e. the additional angular momentum if it so happens that the mass is rotating about a fixed axis through its CM. It is given by ##\vec L_{\text{rotational}}=I_{cm}~\vec{\omega}.## Here, ##I_{cm}## is the moment of inertia about the fixed axis and ##\vec{\omega}## points along the axis.
Note that, in general, the translational angular momentum and the rotational angular momentum need not point in the same direction. For example, as the Earth orbits the Sun it has ##\vec L_{\text{translatonal}}## directed perpendicular to the plane of its orbit (the ecliptic). However, the Earth's ##L_{\text{rotational}## is directed at an angle of 23.4°
away from the perpendicular to the ecliptic.
I hope this helps.