Ebby
- 41
- 14
- Homework Statement
- Find the work done by the braking force and the change in kinetic energy of the car.
- Relevant Equations
- F = m . a
s = v_final^2 - v_initial^2 / 2 . a
W = F . s
delta K.E. = K.E._final - K.E._initial
I'm asking about this with particular reference to the signs of the answers. Here is the question:
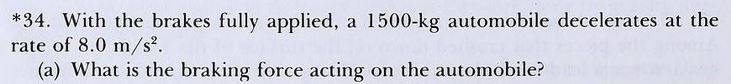
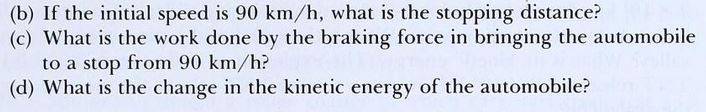
The answers in the back of the book are:
(a) ##1.2 \times 10^4 \text{ N}##
(b) ##39 \text{ m}##
(c) ##4.7 \times 10^5 \text{ J}##
(d) ##4.7 \times 10^5 \text{ J}##
Here's a rough sketch of the situation. I suppose it's not really necessary, but I feel the vectors do emphasise the idea of direction and sign.
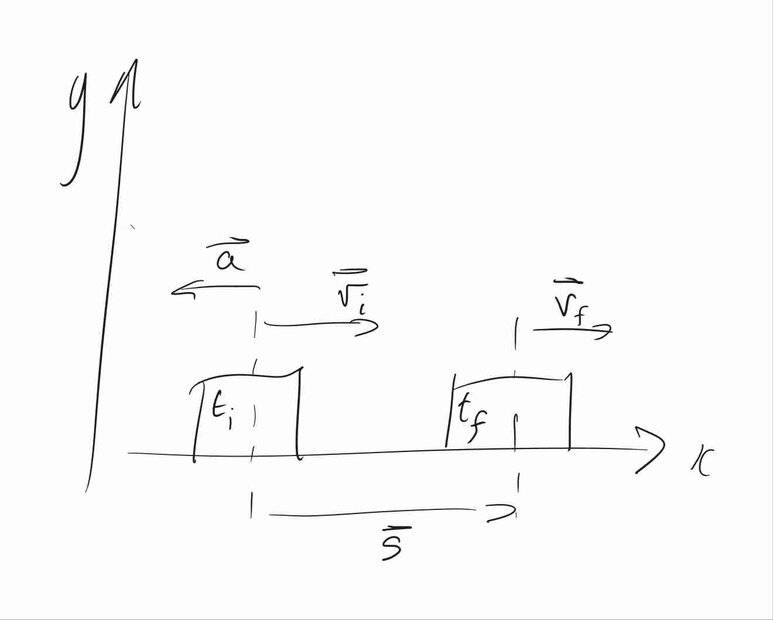
I'll now go through each part, with particular attention to the signs of the answers. I have some disagreements with the book, especially regarding parts (c) and (d).
(a) The acceleration ##\vec a## is the negative ##x## direction, so the component ##F_x## must also be negative:$$F_x = m \cdot a_x = 1500 \cdot -8 = -1.2 \times 10^4 \text { N}$$The book has this answer as being positive. I guess what they're really asking for is the magnitude of the force. OK, accepted.
(b) No problems here. ##|\vec s|## and ##s_x## happen to be the same.$$s_x = \frac {{v_x}_f^2 - {v_x}_i^2} {2 \cdot a_x} = \frac {0 - \left( \frac {90} {3.6} \right)^2} {2 \cdot -8} = \frac {-625} {-16} = 39 \text { m}$$
Oops I accidentally pressed post thread. This isn't finished quite yet. How do I delete it?
The answers in the back of the book are:
(a) ##1.2 \times 10^4 \text{ N}##
(b) ##39 \text{ m}##
(c) ##4.7 \times 10^5 \text{ J}##
(d) ##4.7 \times 10^5 \text{ J}##
Here's a rough sketch of the situation. I suppose it's not really necessary, but I feel the vectors do emphasise the idea of direction and sign.
I'll now go through each part, with particular attention to the signs of the answers. I have some disagreements with the book, especially regarding parts (c) and (d).
(a) The acceleration ##\vec a## is the negative ##x## direction, so the component ##F_x## must also be negative:$$F_x = m \cdot a_x = 1500 \cdot -8 = -1.2 \times 10^4 \text { N}$$The book has this answer as being positive. I guess what they're really asking for is the magnitude of the force. OK, accepted.
(b) No problems here. ##|\vec s|## and ##s_x## happen to be the same.$$s_x = \frac {{v_x}_f^2 - {v_x}_i^2} {2 \cdot a_x} = \frac {0 - \left( \frac {90} {3.6} \right)^2} {2 \cdot -8} = \frac {-625} {-16} = 39 \text { m}$$
Oops I accidentally pressed post thread. This isn't finished quite yet. How do I delete it?
Last edited: