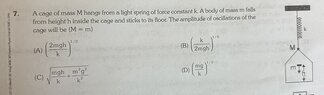Click For Summary
SUMMARY
The discussion centers on the application of energy equations in the context of simple harmonic motion, specifically after a collision where the energy is expressed as mgh/2. Participants emphasize the importance of demonstrating prior effort in problem-solving and adhering to homework guidelines provided by the forum. The use of LaTeX for posting equations is recommended to enhance clarity and precision in mathematical representation.
PREREQUISITES- Understanding of simple harmonic motion principles
- Familiarity with energy conservation concepts
- Basic knowledge of LaTeX for formatting equations
- Awareness of forum homework guidelines
- Study the principles of energy conservation in physics
- Learn how to derive energy equations for simple harmonic motion
- Practice using LaTeX for formatting mathematical equations
- Review forum guidelines for effective problem-solving assistance
Students studying physics, educators teaching mechanics, and anyone seeking to improve their understanding of energy equations in simple harmonic motion.
Similar threads
- · Replies 6 ·
- · Replies 4 ·
- · Replies 20 ·
- · Replies 11 ·
- · Replies 18 ·
- · Replies 20 ·
- · Replies 13 ·