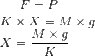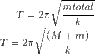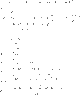- #1
Leo Consoli
- 39
- 5
Homework Statement
The problem is from the Monbukagakusho exam.[/B]
An object of mass M is hanging by a light spring of force constant k from the ceiling. A small ball of mass m which moves vertically upward collides with the object. After the collision, the object and the small ball stick together and oscillate in simple harmonic motion. Before the collision, the object is at rest. The speed of the small ball just before the collision is denoted as v. The acceleration of gravity is denoted as g. Answer the following questions.
1) Find the amount of stretch of the spring from its natural length before the collision.
2) Find the speed of the object and the small ball just after the small ball collides with the object and they stick together.
3) Find the amount of decrease of the sum of kinetic energies of the small ball and the object, before and after the small ball collides with the object.
4) Find the period of the simple harmonic oscillation after the small ball and the object stick together.
5) During the simple harmonic oscillation of the small ball and the object which are stuck together, the spring is at its natural legth when the object is at its highest position. Find the kinect energy of the ball just before it collides with the object.
Homework Equations
Hooke's law.
Period of a harmonic oscilator.
Conservation of momentum.
Cinetic energy.
The Attempt at a Solution
I was able to solve from 1 to 4, but I left if here because I think it can help solving 5, here is what I did from 1 to 4:
1)
2)
3)
4)
Now as for the 5 question I can't really find an answer because according to the formula, the kinectic energy would be mv^2/2, but the alternatives are very different from this, the collision is inelastic so mechanic energy is not conserved so I can't find a relation between the mechanic energy of the ball, and the mechanic energy of the oscilating system with the ball and the object together, here are the alternatives. Thanks for any help.