Simple Harmonic Motion - what is its new period

[mattmannmf]

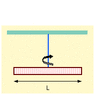
A uniform meter stick is hung at its center from a thin wire. It is twisted and oscillates with a period of 5 s. The meter stick is then sawed off to a length of 0.76 m, rebalanced at its center, and set into oscillation.

what is its new period
I= 1/12 mL^2

equation: T= 2 pi * sqrt (I/k)
where T= 5
L= 1

I solved for K in terms of m (mass)...where i got k=7.599 m

then i replugged it into the same equation but where
T= unknown (trying to find)
L=.76

the mass cancels out and my answer gives me 3.8... which is wrong when i checked.

The only thing i can see is that I am using the wrong "I" for using the same equation 2nd time when i replugged it in. Should i be using the parallel axis theorem where

I= 1/12 mL^2 + Md^2
(since its not revolving around its center of mass)
L=1
d= .76

when i tried that i got my answer to be 6.28...wrong again

 

[denverdoc]

The eqn for I for a rectangular plate is m(l^2+h^2)/12 where l and h are length and height respectively. It is revolving about the center of mass in both cases so no need for parallel axis theorum. You may need to solve for height, if the factor 0.76^3 isn't giving the right answer (remember the mass is being reduced by 24% as well).

BTW, neglecting the height, I got an answer of T=3.31s

 

[kerimek]

It seems like you are on the right track with using the parallel axis theorem. However, the formula for the moment of inertia of a uniform meter stick is actually I=1/12 mL^2, where m is the mass of the meter stick and L is the length. So for the new length of 0.76 m, the moment of inertia would be I=1/12 * m * (0.76)^2. You can then use this value for I in the equation T=2pi*sqrt(I/k) to solve for the new period. Hope this helps!