Simplification Help: Can't Simplify Further?

  • Thread starter Thread starter 7yler
  • Start date Start date
Click For Summary
SUMMARY

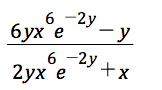
The discussion centers on the implicit differentiation of the equation x6e-2y = ln(xy) to find dy/dx. The user believes they have simplified the expression to 3 - (3x + y) / (x(2yx5e-2y - 1)), but doubts its correctness. Another participant suggests recalculating the partial derivative with respect to y to verify the solution. The key takeaway is the importance of accurately applying implicit differentiation techniques in calculus.

PREREQUISITES
  • Understanding of implicit differentiation
  • Familiarity with logarithmic functions
  • Knowledge of partial derivatives
  • Basic calculus concepts
NEXT STEPS
  • Review implicit differentiation techniques in calculus
  • Study the properties of logarithmic functions
  • Learn how to calculate partial derivatives
  • Practice solving similar implicit differentiation problems
USEFUL FOR

Students studying calculus, educators teaching implicit differentiation, and anyone seeking to improve their understanding of derivatives and logarithmic functions.

7yler
Messages
31
Reaction score
0
I have worked a question down to this, but I am not sure how to simplify any further.

rcohgn.png
 
Physics news on Phys.org
I think that has been simplified enough. I see no way to simplify it any further...
 
= 3 - \frac{3x+y}{x\left(2yx^5 e^{-2y} -1\right)} ??

But that's not really simplification :))
 
The original question was: suppose x^{6}e^{-2y}=ln(xy)

Find \frac{dy}{dx} by implicit differentiation.

That is the answer that I have come to, but it is said to be wrong.
 
And can you posts what you did to get to that solution?
 
Well, you should calculate once more the partial derivative wrt y.
 

Similar threads

Special Comparison Test For Infinite Series
  • · Replies 4 ·
Replies
4
Views
2K
Antiderivative of Heaviside step function with absolute-value-argument
  • · Replies 2 ·
Replies
2
Views
2K
Maple Why can't Maple simplify this further?
  • · Replies 10 ·
Replies
10
Views
4K
Help with Vector Multiplication please
  • · Replies 7 ·
Replies
7
Views
2K
Intuition about simplifying this expression
  • · Replies 2 ·
Replies
2
Views
1K
Power Rule Proof: Get Help with Line 3 to Line 4
  • · Replies 17 ·
Replies
17
Views
1K
Simplifying expressions using Euler's formula
  • · Replies 1 ·
Replies
1
Views
2K
Induction with binomial coefficient
  • · Replies 15 ·
Replies
15
Views
3K
Infinite Series (Geometric) Problem
  • · Replies 4 ·
Replies
4
Views
2K
MATLAB Streamline Symbolic Derivatives with MATLAB's Simplify Operation
  • · Replies 4 ·
Replies
4
Views
3K