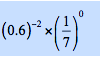SUMMARY
The discussion focuses on the simplification of expressions involving exponents using the Laws of Exponents. Participants emphasize the importance of understanding these laws to evaluate expressions without a calculator. Specific techniques for simplifying expressions, such as combining like bases and applying exponent rules, are highlighted as essential skills. The conversation encourages users to share their attempts and seek guidance on specific problems.
PREREQUISITES
- Laws of Exponents
- Basic algebraic manipulation
- Understanding of mathematical notation
- Familiarity with simplifying expressions
NEXT STEPS
- Study the Laws of Exponents in detail
- Practice simplifying expressions with different bases
- Explore advanced exponent rules, such as negative and fractional exponents
- Engage in problem-solving exercises without a calculator
USEFUL FOR
Students, educators, and anyone looking to enhance their skills in algebra and mathematical expression simplification.