SUMMARY
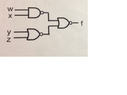
The discussion focuses on simplifying a Boolean circuit represented by the equation f = (W NAND X) NOR (Y NOR Z). The participants apply De Morgan's Theorem to transform the expression into a simplified Sum of Products (SoP) form. The final simplified equation is f = wx(y + z), demonstrating the effective use of Boolean algebra techniques to achieve simplification.
PREREQUISITES
- Understanding of Boolean algebra concepts
- Familiarity with De Morgan's Theorem
- Knowledge of NAND and NOR gate operations
- Ability to manipulate logical expressions in SoP form
NEXT STEPS
- Study advanced Boolean algebra techniques for circuit simplification
- Learn about the practical applications of NAND and NOR gates in digital circuits
- Explore further examples of De Morgan's Theorem in circuit design
- Investigate tools for simulating Boolean circuits and verifying simplifications
USEFUL FOR
Students and professionals in electrical engineering, computer science, and anyone involved in digital circuit design and optimization.