LCSphysicist
- 644
- 163
- Homework Statement
- All below
- Relevant Equations
- All below
Sketch a qualitatively accurate graph of the entropy of a substance
as a function of temperature, at fixed pressure. Indicate where the
substance is solid, liquid, and gas . Explain each feature of the graph briefly.
What you think about?:
dU = -P*dV + Q*dS (1)
V = C*T => dV = C*dT
Nfk*dT/2 + P*C*dT = Q*dS
Nfk/2 + P*C = Q*(dS/dT)
For a solid, i assumed f = 3, for a liquid f = 5 and for the gas, f > 5 (i think is not necessary say the obvious this is a rough approximation)
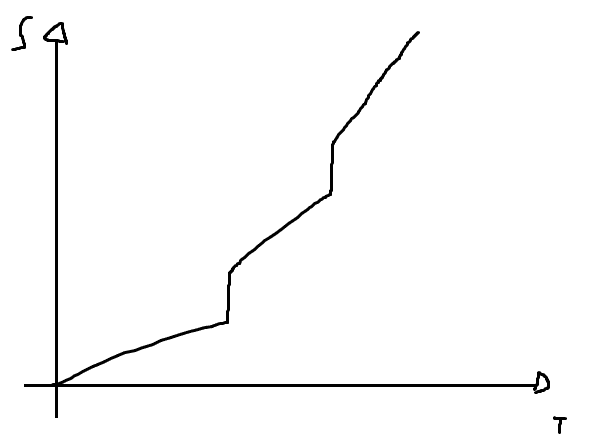That would be the result.
as a function of temperature, at fixed pressure. Indicate where the
substance is solid, liquid, and gas . Explain each feature of the graph briefly.
What you think about?:
dU = -P*dV + Q*dS (1)
V = C*T => dV = C*dT
Nfk*dT/2 + P*C*dT = Q*dS
Nfk/2 + P*C = Q*(dS/dT)
For a solid, i assumed f = 3, for a liquid f = 5 and for the gas, f > 5 (i think is not necessary say the obvious this is a rough approximation)