Sketch Inequality: Region of $(x,y)$ Points

[Dethrone]

From the differentiation section of my calculus textbook:

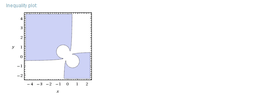
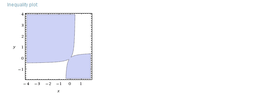
Sketch the region in the plane consisting of all points $(x,y)$ such that
$$2xy\le\left| x-y \right|\le x^2+y^2$$

I have tried to look at the cases:

Case 1: $x>y$

$$2xy\le x-y\le x^2+y^2$$
$$0\le (x-y)-2xy\le x^2+y^2-2xy$$

Now I have tried to split that by looking at what it needs to satisfy, but I'm not sure if this is correct:
1)
$$0\le x^2+y^2-2xy$$
$$0\le (x-y)^2$$
$$y\le x$$

2)

$$0\le (x-y)-2xy$$

3)

$$x-y \le x^2 +y^2$$

But something doesn't seem right...any hints? :D

 

[ineedhelpnow]

hey (Wave)
the inequality can be divided into $x^2+y^2-\left| x-y \right|\ge 0$
you can start by sketching the curve $x^2+y^2-\left| x-y \right|= 0$

sketch the graph and you'll notice it looks like two circles attached kind of.
then take a test point like (0.5,-1) inside the loop. put it into the inequality $x^2+y^2-\left| x-y \right|\ge 0$ solve that and you'll find that the solution is false since the number you come up with on the LHS will be less than 0 instead. so you shade the region outside of the loop.
then sketch the curve $2xy-\left| x-y \right|=0$
then take the test point (0.5,-1) and plug into $2xy-\left| x-y \right|\le 0$
the solution to this is true since the left side IS less than the right sides so you sketch the inside of the curve.
now just merge the two sketches together.

 

[Dethrone]

Thanks so much Pippy! (flower)

I got it now...and it required a bit of neat factoring too :D

Like:

$$x^2+y^2-x+y=0$$
$$x^2-x+y^2+y=0$$
$$\left(x-\frac{1}{2}\right)^2+\left(y+\frac{1}{2}\right)^2-\frac{1}{2}=0$$

 

[MarkFL]

Thanks so much Pippy! (flower)

I got it now...and it required a bit of neat factoring too :D

Like:

$$x^2+y^2-x+y=0$$
$$x^2-x+y^2+y=0$$
$$\left(x-\frac{1}{2}\right)^2+\left(y+\frac{1}{2}\right)^2+\frac{1}{2}=0$$

I am certain you mean:

\(\displaystyle \left(x-\frac{1}{2}\right)^2+\left(y+\frac{1}{2}\right)^2-\frac{1}{2}=0\)

 

[ineedhelpnow]

Please post your solution so that we can have it as a reference for others who may need help

Thank you (Giggle)

 

[Dethrone]

Here is my solution, as promised:

Problem:

$$2xy\le |x-y| \le x^2+y^2$$

Solution:

$$2xy\le |x-y| \le x^2+y^2$$

Focusing on the right side of the inequality:
$$|x-y| \le x^2+y^2$$
$$0\le x^2+y^2-|x-y|$$

Case 1: \(\displaystyle x \ge y\)	Case 2: \(\displaystyle x<y\)
$$x^2+y^2-(x-y) \ge 0$$ $$\left(x-\frac{1}{2}\right)^2+\left(y+\frac{1}{2}\right)^2 \ge \frac{1}{2}$$	$$x^2+y^2+(x-y) \ge 0$$ $$\left(x+\frac{1}{2}\right)^2+\left(y-\frac{1}{2}\right)^2 \ge \frac{1}{2}$$

Both of these cases take the shape of a circle and the region of interest is outside of the circle.

View attachment 3724
Fig. 1

Now, focusing on the left side of the inequality:

$$2xy \le |x-y|$$
$$2xy-|x-y| \le 0$$

Case 1: \(\displaystyle x \ge y\)	Case 2: \(\displaystyle x < y\)
$$2xy-(x-y) \le 0$$ $$-x+2xy+y \le 0$$ Rearranging, we see that: $$x>-\frac{1}{2} \text{ when } y \le \frac{x}{2x+1}$$ $$x<-\frac{1}{2} \text{ when } y \ge \frac{x}{2x+1}$$	$$2xy+(x-y) \le 0$$ $$2xy+x-y \le 0 $$ Similarly, $$x>\frac{1}{2} \text{ when } y\le -\frac{x}{2x-1}$$ $$x<\frac{1}{2} \text{ when } y \ge -\frac{x}{2x-1}$$

View attachment 3725
Fig. 2

Concatenating our results, we obtain the below graph. (Note that in order to satisfy both plots, fig. 1 cuts into fig. 2.)

View attachment 3723

Thanks, Pippy! :D