bwpbruce
- 60
- 1
$\textbf{Problem:}$
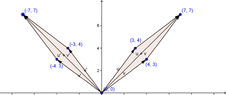
Let $T: \mathbb{R}^2 \rightarrow \mathbb{R}^2$ be the linear transformation that reflects each point through the $x_2$ axis. Make two sketches that illustrate properties of linear transformation.
$\textbf{Solution:}$
Let $T(\textbf{x}) = \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} -x_1 \\ x_2 \end{bmatrix}$
Let
$\textbf{u} = \begin{bmatrix} 3 \\ 4 \end{bmatrix}, \textbf{v} = \begin{bmatrix} 4 \\ 3 \end{bmatrix}$
And $\textbf{u + v} = \begin{bmatrix} 7 \\ 7 \end{bmatrix}$
Then
$T\textbf{u} = \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} 3 \\ 4 \end{bmatrix} = \begin{bmatrix} -3 \\ 4 \end{bmatrix}$
$T\textbf{v} = \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} 4 \\ 3 \end{bmatrix} = \begin{bmatrix} -4 \\ 3 \end{bmatrix}$
$T\textbf{u + v} =\begin{bmatrix} -7 \\ 7 \end{bmatrix}$
$T\textbf{(0)} = \textbf{0}$
View attachment 3893
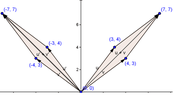
Let $T: \mathbb{R}^2 \rightarrow \mathbb{R}^2$ be the linear transformation that reflects each point through the $x_2$ axis. Make two sketches that illustrate properties of linear transformation.
$\textbf{Solution:}$
Let $T(\textbf{x}) = \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} -x_1 \\ x_2 \end{bmatrix}$
Let
$\textbf{u} = \begin{bmatrix} 3 \\ 4 \end{bmatrix}, \textbf{v} = \begin{bmatrix} 4 \\ 3 \end{bmatrix}$
And $\textbf{u + v} = \begin{bmatrix} 7 \\ 7 \end{bmatrix}$
Then
$T\textbf{u} = \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} 3 \\ 4 \end{bmatrix} = \begin{bmatrix} -3 \\ 4 \end{bmatrix}$
$T\textbf{v} = \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} 4 \\ 3 \end{bmatrix} = \begin{bmatrix} -4 \\ 3 \end{bmatrix}$
$T\textbf{u + v} =\begin{bmatrix} -7 \\ 7 \end{bmatrix}$
$T\textbf{(0)} = \textbf{0}$
View attachment 3893