Sliding Rod and Rotating Disc Question

[aerograce]

Homework Statement

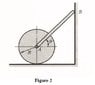
A uniform rod AB of length L and mass m1 is connected by a pin joint to the center of a
uniform disc of radius R and mass m2.
The system is placed in a vertical plane (as shown in Figure 2) and released from rest with
θ=45°.
(a) Draw the free-body diagrams for the rod and the disc.
(b) Find the acceleration of the point B at the instant when the system is released.
You may assume that the pin joint and the vertical wall are frictionless, and the disc rolls
without slipping on the horizontal ground.

Homework Equations

T=Iα;
[a][/B]=[a][/A] + w×(w×[r][/(B/A)]+w'×[r][/(B/A)]

The Attempt at a Solution

My attempt is to first use equilibrium to calculate the static friction force acting on the ground and then through fR=T=Iα to calculate the angular acceleration of point A. This will then help us obtain acceleration of A. Then use the above formula to relate acceleration of B to acceleration of A. But I realize this may be untrue since the system is not in equilibrium initially.

 

[haruspex]

I realize this may be untrue since the system is not in equilibrium initially.

Quite so, that will not work.
Did you draw the free body diagrams?
List the forces acting on each (including directions).
Let the initial angular acceleration of the disk be $\alpha$. What is its horizontal acceleration?
What accelerations does that imply for the rod?
What equations can you write down relating these accelerations to the forces?

 

[aerograce]

Hello. I have drawn free body diagram as follow. The horizontal acceleration of a will be α*R. And this acceleration can be related to point B with formula
[a][/B]=[a][/A] + w×(w×[r][/(B/A)]+w'×[r][/(B/A)]. But I think when I write down equations, I discover too many unknowns to be solved. Could you explain a bit more to me? Thank you so much for your time

 

[haruspex]

Hello. I have drawn free body diagram as follow. The horizontal acceleration of a will be α*R. And this acceleration can be related to point B with formula
[a][/B]=[a][/A] + w×(w×[r][/(B/A)]+w'×[r][/(B/A)]. But I think when I write down equations, I discover too many unknowns to be solved. Could you explain a bit more to me? Thank you so much for your time

You should have six unknowns: four normal forces, a frictional force and an acceleration. (Or maybe more accelerations, but they're all determinable by anyone of them.)
There are six equations: X, Y and moments for each of the two objects. Should be enough.

 

[aerograce]

You should have six unknowns: four normal forces, a frictional force and an acceleration. (Or maybe more accelerations, but they're all determinable by anyone of them.)
There are six equations: X, Y and moments for each of the two objects. Should be enough.

May I know, when writing the rotational equilibrium equation, should I list moment equilibrium about its center of gravity? I am confused because since center of gravity of the link AB is not a fixed point, if write moment equilibrium about its center of gravity, the angular acceleration has to be about its center of gravity too, but the center of gravity itself is moving. This sometimes confuses me when exam questions ask me to decide angular acceleration or angular velocity of a certain link, I find it not a correct expression coz it didnt specify angular acceleration or velocity about which point.

Hope you can clarify my doubts! Thank you so much

 

[haruspex]

May I know, when writing the rotational equilibrium equation, should I list moment equilibrium about its center of gravity? I am confused because since center of gravity of the link AB is not a fixed point, if write moment equilibrium about its center of gravity, the angular acceleration has to be about its center of gravity too, but the center of gravity itself is moving. This sometimes confuses me when exam questions ask me to decide angular acceleration or angular velocity of a certain link, I find it not a correct expression coz it didnt specify angular acceleration or velocity about which point.

Hope you can clarify my doubts! Thank you so much

I assume you did not mean 'equilibrium' here.
In a dynamic set-up, safest is to take moments about a point fixed in space. Taking moments of forces acting on a rigid body about that body's mass centre should also be fine, as is taking moments about the body's instantaneous centre of rotation. Anything else may produce a wrong answer. See section 5 in https://www.physicsforums.com/insights/frequently-made-errors-mechanics-moments/