MHB Slope of Level Curve b at Point B: How to Determine It?

[Yankel]

Hello all,

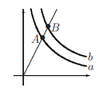
In the attached photo, I have two level curves of the function:

\[f(x,y)=x^{\alpha }y^{\beta }\]

where alpha and beta are constants. In addition, I have the line

\[y=2x\]

It is known that the slope of the level curve a at the point A is -3. I need to find the slope of the level curve b at the point B.

Any ideas or hints ? Thanks !

View attachment 2350

 

[Ackbach]

Level curves are where $f(x,y)$ is a constant, right? So, for curve $a$, why not set $a=x^{\alpha}y^{\beta}$. Could you find $y'$?

 

[Yankel]

yes... it is

\[\frac{\partial y}{\partial x}=-\frac{\alpha x^{\alpha -1}}{\beta y^{\beta -1}}\]

how do I proceed from here ?

 

[Ackbach]

So what could you say about point $A$? Could you find its coordinates, perhaps? You know it's on both the level curve and the line $y=2x$.

 

[Yankel]

How can I find the coordinates of A if I have 2 unknown constants ?

I think that it should be A(a/2,a), but I am not sure, and don't know how to proceed even if it is true...

 

[Yankel]

The final answer by the way should be -3, I really don't know how to get there.
(Sadface)

 

[Ackbach]

How can I find the coordinates of A if I have 2 unknown constants ?

I think that it should be A(a/2,a), but I am not sure, and don't know how to proceed even if it is true...

For point $A$ you have the condition:
$$-3=-\frac{\alpha x^{\alpha-1}}{\beta (2x)^{\beta-1}}. $$
The target variable is $m$, where
$$-m=-\frac{\alpha x^{\alpha-1}}{\beta (2x)^{\beta-1}},$$
where the $x$'s here are not necessarily the same as the $x$'s above. So here, you see we've used the fact that $y=2x$. We have not used the fact that we're on level curves. That may or may not be helpful, as it introduces another unknown. Can you try to work out a ratio, where something cancels? Try simplifying the expression we've got.

 

[Yankel]

this is a complicated one, isn't it ? (Whew)

Level curves will add another unknown in addition to alpha and beta, which are already a problem.

I tried simplifying your expression, there is not much I can do with it.

\[3=\frac{\alpha }{\beta }\cdot \frac{1}{2^{\beta -1}}\cdot x^{\alpha -\beta }\]

But if the x's are not the same x's (slightly confusing), how can it help me when I replace 3 for m ? Logic say that somehow I am supposed to use 3, otherwise I wouldn't be given it.

 

[Opalg]

yes... it is

\[\frac{\partial y}{\partial x}=-\frac{\alpha x^{\alpha -1}}{\beta y^{\beta -1}}\]

how do I proceed from here ?

You seem to have differentiated this wrongly. The level curve is $x^\alpha y^\beta = a$. If you use implicit differentiation on that equation, you get $(\alpha x^{\alpha-1})y^\beta + x^\alpha \bigl(\beta y^{\beta-1}\frac{dy}{dx}\bigr) = 0.$ Cancel $x^{\alpha-1}y^{\beta-1}$ and solve for $\frac{dy}{dx}$ to get $\dfrac{dy}{dx} = \dfrac{\alpha y}{\beta x}$. At each point on the line $y=2x$, that has the same value $\dfrac{2\alpha}{\beta}.$

 

[Yankel]

Yes, you are right ! (Blush) I did it all wrong.

I have calculated the derivative again, and I got it similar to yours, but with a minus before the expression (dy/dx = -(Fx/Fy)).

Still, I can't see how to progress from here. I mean, even if I do replace y for 2x, and by that x also goes, I still have alpha and beta. What I still miss here is how to use the information about -3 to find what I want.

The expression I got after replacing y=2x is independent of x. So if for level curve a, the slope is -3, shouldn't it be also -3 for b ? I don't get why it is 3 (unless the book answer is incorrect).

 

[Opalg]

Yes, you are right ! (Blush) I did it all wrong.

I have calculated the derivative again, and I got it similar to yours, but with a minus before the expression (dy/dx = -(Fx/Fy)).

Still, I can't see how to progress from here. I mean, even if I do replace y for 2x, and by that x also goes, I still have alpha and beta. What I still miss here is how to use the information about -3 to find what I want.

The expression I got after replacing y=2x is independent of x. So if for level curve a, the slope is -3, shouldn't it be also -3 for b ? I don't get why it is 3 (unless the book answer is incorrect).

You're right, I left out a minus sign. It should be $\dfrac{dy}{dx} =- \dfrac{\alpha y}{\beta x}$. You said in comment #6 that the answer should be $-3$, so presumably that is what the book says. The slope of the level curve at $B$ is clearly negative, as you can see from the diagram. So the answer could not possibly be $3$.

 

[Yankel]

This was getting confusing, so I checked again, and the answer in the book is 3 and not -3, I was wrong in answer #6.

I do get what you say, it must be negative...

But just to understand, is it correct that it's -3 because the expression is not dependent on x, and thus at every point on y it will be -3 ?

 

[Deveno]

We can only determine the slope on the level curve $b$ when we know the ratio of $y$ to $x$, that is to say: which line it lies on.

For BOTH level curves, we have:

$\dfrac{dy}{dx} = -\dfrac{\alpha y}{\beta x}$

which depends on just two things: the constant $-\dfrac{\alpha}{\beta}$ and the ratio $\dfrac{y}{x}$.

Put another way, on any line through the origin, the tangent lines through the intersection points are parallel, which the drawing suggests as well.