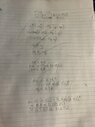So confused by these multi-step questions, free fall related:

[ConfusedStudentx10E9]

Homework Statement

You throw a ball off a cliff with an initial velocity of 25.0 m/s. You start a stopwatch as you throw the ball: the ball rises then falls, and passes your level again after t=0.752 s has elapsed. Sadly, you lose sight of the ball as it falls, and therefore cannot time when the ball hits the ground. Later you find that the ball landed 112 m from the base of the cliff. Assuming that the ball did not "bounce" after landing on the sand, how high up was the cliff? Assume that the ball started exactly 1.60 m above the edge of the cliff.

Relevant Equations

I have no idea and thats the problem.

Tried making many squiggles, I don't understand the concept of finding a distance or position based on a time for part of the flight. I have 2 other similar questions and I haven't been able to make any progress on any of them.

I attached a photo of my scribbles, which are all obviously useless and I'm sure I'm literally just making stuff up to try and make an equation work.

Any help is much appreciated!

** note we assume no friction or resistance. I know acceleration is just gravity.

 

[PeroK]

Let's focus on the first part of the problem. You know the initial velocity and the time to fall back to the initial level. Which quantities does this allow you to calculate?

 

[PeroK]

Note: this is a two dimensional problem.

 

[ConfusedStudentx10E9]

Let's focus on the first part of the problem. You know the initial velocity and the time to fall back to the initial level. Which quantities does this allow you to calculate?

i could calculate the velocity at the time given, but that's not helpful.

I could calculate its distance on the x-axis at the given time?

I'm honestly not sure.

 

[haruspex]

i could calculate the velocity at the time given, but that's not helpful.

I could calculate its distance on the x-axis at the given time?

I'm honestly not sure.

just think about the vertical aspect of the motion. Given the time to return to the original height, what can you determine?

 

[PeroK]

i could calculate the velocity at the time given, but that's not helpful.

I could calculate its distance on the x-axis at the given time?

I'm honestly not sure.

Okay, but the full problem is a fairly advanced projectile motion problem. You should have built up experience and knowledge from previous problems.

Have you done any projectile motion problems before?

 

[ConfusedStudentx10E9]

Okay, but the full problem is a fairly advanced projectile motion problem. You should have built up experience and knowledge from previous problems.

Have you done any projectile motion problems before?

Honestly no, this is a first-year college course I'm taking and I haven't taken high school physics in over 8 years so I do not remember anything. this is chapter 2 of this course, the first chapter was just terminology, sig figs, and vectors. I'm totally lost and don't even know where to start to try and catch up. I have the first quiz on Monday, I've hired a tutor, and I've spent hours trying to catch up watching videos on youtube but I feel so lost.

 

[PeroK]

Honestly no, this is a first-year college course I'm taking and I haven't taken high school physics in over 8 years so I do not remember anything. this is chapter 2 of this course, the first chapter was just terminology, sig figs, and vectors. I'm totally lost and don't even know where to start to try and catch up. I have the first quiz on Monday, I've hired a tutor, and I've spent hours trying to catch up watching videos on youtube but I feel so lost.

That's an honest answer. Unfortunately, this medium is not suitable for teaching you a subject from the ground up.

I think you need access to simpler problems to get you started.

That said, if we have initial velocity and time to fall back, then we can calculate: the vertical component of velocity, hence the horizontal component, hence the max height ( if needed) and the horizontal range.

You first need to understand how to use the equations of projectile motion to do that.

 

[PeroK]

Problems that involve projecting an object off a cliff are the next step.

 

[ConfusedStudentx10E9]

That's an honest answer. Unfortunately, this medium is not suitable for teaching you a subject from the ground up.

I think you need access to simpler problems to get you started.

That said, if we have initial velocity and time to fall back, then we can calculate: the vertical component of velocity, hence the horizontal component, hence the max height ( if needed) and the horizontal range.

You first need to understand how to use the equations of projectile motion to do that.

Would you still be able to go over this particular example, even just the steps and equations used? Obviously, I'm backtracking with the tutor to try and understand everything but I have the first quiz on Monday, while I don't expect to do well I can at least hope to get partial marks for being able to come up with something. I do learn best from examples, and part of the reason I'm struggling with this is because even the instructor for this class has not done an example like this. All of her examples have had the total time as a known.

I understand I'm going to have to work extremely hard to understand this material, but I would still really appreciate a previous problem to refer to if possible.

 

[PeroK]

For 2D motion under gravity you have equations of motion in the two directions:
$$y = y_0 + u_yt - \frac 1 2g t^2$$$$x = x_0 + u_xt$$Note that gravity affects only the $y$ component of velocity, so the $x$ component of velocity is constant:$$v_y = u_y - gt$$$$v_x = u_x$$

 

[Steve4Physics]

Hi @ConfusedStudentx10E9

You might find the following 3 videos I made some time ago useful. They are an introduction to projectile motion - starting from the basics. They include exercises to try for yourself during the video and the worked solutions.