Solution needed for 7x7 Matrix/Sudoku (with additional restriction rules)

[skavorn]

Ok what I'm trying to do is create a table where football tactics counter each other in a numbered order. Such as like a filled in order of the below table...

This can be simplified into a 7x7 matrix table such as the below (by renaming the tactics, 1-7)

We have 3 rules that need to be adeared to:
1) There needs to be a different tactic in each row and each column. Essentially making like a sudoku puzzle.
2) Rows can't have the same 2 numbers reversed. i.e. 6, 7 should not be 7,6 elsewhere

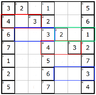
3) Every number entered needs to have it's opposite entered. i.e. if Attacking is 2nd strongest vs Balanced, then Balanced is 2nd weakest vs Attacking. Here's an illustrated example...

I've been using this to assist me KenKen Solver, however it doesn't take additional rules 2 & 3 into consideration.

Is this solvable?

 

[Unknown008]

I'm not sure I understand rule #2. You circled (1,2), (2,1) and (6,5), (5,6). I get those. But you put an arrow on (5,6) in column '6' and columns '5' and '4'?

And what do the colours mean? Does 1 (red) mean strongest?

If so, there obviously is a tactic strong against another, but weak against a different tactic, which itself is strong against the first tactic.

Eg. We know that:
5 > 3 (row 1)
3 > 2 (row 6)
2 > 4 (row 4)
4 > 5 (row 7)

Where we see that a tactic (4) which is weaker than tactics themselves weaker than 5 is actually stronger than tactic 5. Or is there something I didn't get here?

 

[skavorn]

I'm not sure I understand rule #2. You circled (1,2), (2,1) and (6,5), (5,6). I get those. But you put an arrow on (5,6) in column '6' and columns '5' and '4'?

And what do the colours mean? Does 1 (red) mean strongest?

If so, there obviously is a tactic strong against another, but weak against a different tactic, which itself is strong against the first tactic.

Eg. We know that:
5 > 3 (row 1)
3 > 2 (row 6)
2 > 4 (row 4)
4 > 5 (row 7)

Where we see that a tactic (4) which is weaker than tactics themselves weaker than 5 is actually stronger than tactic 5. Or is there something I didn't get here?

Essentially I mean anytime two columns have a row next to each other I don't want them matching otherwise one tactic has the same two advantages/disadvantages, just in reversed order. I do not want this. I don't want attacking best against, balanced second best, and then attacking second best, balanced best in another tactic.

Yes colours represent strength, green is strongest, red is weakest

Numbers in the middle are against themselves, so there is no advantage(null)

 

[Unknown008]

If I got the rules right, how about:

View attachment 786

I started with your example but it lead to nowhere. From there I tried '2' (I couldn't put '1' since there was already '1' in the row) at the top right corner and everything magically fell into place.

I tried others but I quickly spotted illegal 'moves'. Maybe I missed one here, and if so, I don't believe there's a solution.

 

[skavorn]

Just checked it out and it works perfectly. Thank you so much!

Additional question, is there multiple solutions to this or is there only one?

Also how did you work it out, was it just manual trial and error?

 

[Unknown008]

I couldn't find any more solutions, sorry.

And yes, it was trial and error on the first number only. Then using Rules 2 and 3, I put all the numbers one after the other.

Say, I put 2 in the upper left corner, it means I look for 2 and 3 everywhere in the grid and put them in that order.

Like this:

View attachment 787

And here you see that we get a couple other patterns (boxed in red) which I can use to fill in the blue box squares.

You will also notice another pattern (green) that you can use. You go on like this and you'll be able to fill in all the squares.

 

[skavorn]

That's been really helpful, thank you so much