Solve Angular Speed of Rotating Rod: Conservation of Energy

[rasensuriken]

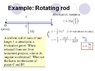
The question is as the attachment...
May i know if i want to find the angular speed of the rod when it inclined at certain angle, or at horizontal, can i use the \varpi^2=\varpi_0^2+2\alpha\vartheta?

Attempt: I used it, and used conservation of energy, the latter produces right answer, but i don't know why first one won't work. Any clues?

 

[tiny-tim]

Hi rasensuriken!

I can't read your formula … but, looking at the .jpg, I don't think the angular acceleration, α, is constant (because the torque from the weight is different for different angles).

So a formula using constant α won't work!

 

[kkrizka]

tiny-tim is right, the author of the JPEG image made a mistake. He forgot that the torque is a cross product of radius and the force, which depends on the angle. And the angle changes as the whole thing swings down, so the alpha should be more like:
\tau = MG\frac{L}{2} \sin{\omega t}
Which, as you can see, depends on the time and so is not constant. The conservation of energy worked because it does not care about the acceleration at any point, but only on the initial and final conditions.

 

[tiny-tim]

Hi kkrizka!

No, he didn't forget … he only asked for the inital values, for which his equations are correct.

The question in the OP is rasensuriken boldly going further!

 

[kkrizka]

Hi kkrizka!

No, he didn't forget … he only asked for the inital values, for which his equations are correct.

The question in the OP is rasensuriken boldly going further!

Ah whoops, I've been reading too many phys problems lately and they are starting to get mixed up. :P

 

[rasensuriken]

ya...i also just thought of that...the acceleration is not constant...because the L/2 relative to the center of mass keep on changing...thanks!