A falling rotating rod strikes a ball of mass M....

[Nexus99]

Homework Statement

is this correct?

Relevant Equations

conservation of energy, angular momentum ecc.

A homogeneous rod of length l and mass m is free to rotate in a vertical plane around a point A, the constraint is without friction.
Initially the rod is stopped in the position of unstable equilibrium, therefore it begins to fall rotating around A and hits, after a rotation of $\pi$ , a ball of mass M resting on a plane at a distance l from the constraint.
The collision is elastic, calculate:
1) Rotational speed of the rod a moment before the collision
2) How much mass M should be so that the rod remain stationary after the collision
3) Magnitude of the impulse transferred by the constraint in the previous case

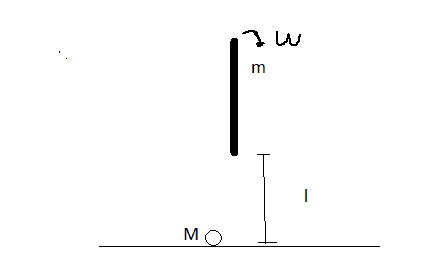
I forgot to draw point A, but how you can image is where the rod begin looking the drawing from bottom to top

I did the problem in this way
1) Conservation of energy,
$E_i = mg \frac{3}{2} l$
$E_f = mg \frac{1}{2} l + \frac{1}{2} I \omega^2$ where $I = \frac{ML^2}{3}$
and i got $\omega = \sqrt{\frac{6g}{l}}$

2) Conservation of energy and angular momentum (calculating momentum from point A)

$mg \frac{1}{2} l + \frac{1}{2} I \omega^2 = \frac{1}{2}Mv^2$
$I \omega = Mv l$
and i got:
$v = \sqrt{6 g l}$ and $M = \frac{m}{3}$

3) $J_R = - \Delta p_M$ since the center of mass of the rod is not moving after the collision
$J_R = - \frac{m}{3}\sqrt{6 g l}$
is the problem correct?

 

[PeroK]

Can you sort your Latex: use double hashes, not single hanshes.

 

[Nexus99]

Sorry, i edited my previous post

 

[PeroK]

Sorry, i edited my previous post

The answers to parts 1) and 2) look correct. Can you explain the answer to 3)? Especially in terms of the total linear momentum of the system.

 

[PeroK]

2) Conservation of energy and angular momentum (calculating momentum from point A)

$mg \frac{1}{2} l + \frac{1}{2} I \omega^2 = \frac{1}{2}Mv^2$

You got the right answer, but this equation should have the PE of the rod on both sides of the equation. Or, better, left out altogether, as it's the same before and after the collision.

 

[Nexus99]

You got the right answer, but this equation should have the PE of the rod on both sides of the equation. Or, better, left out altogether, as it's the same before and after the collision.

Trying to explain the my solution i realized that i made a mistake:
$J_R = \Delta p_{tot}$ where $p_{tot}$ stands fot total momentum of the system, not only the impulse given by the ball.
So i got:
$p_{tot} = \frac{m}{3}v - m \omega \frac{l}{2} = -m\frac{\omega}{6}l$

 

[PeroK]

Trying to explain the my solution i realized that i made a mistake:
$J_R = \Delta p_{tot}$ where $p_{tot}$ stands fot total momentum of the system, not only the impulse given by the ball.
So i got:
$p_{tot} = \frac{m}{3}v - m \omega \frac{l}{2} = -m\frac{\omega}{6}$

Be careful. That answer is dimensionally inconsistent.

 

[Nexus99]

Be careful. That answer is dimensionally inconsistent.

sorry, i forgot an l, now should be ok

 

[PeroK]

Trying to explain the my solution i realized that i made a mistake:
$J_R = \Delta p_{tot}$ where $p_{tot}$ stands fot total momentum of the system, not only the impulse given by the ball.
So i got:
$p_{tot} = \frac{m}{3}v - m \omega \frac{l}{2} = -m\frac{\omega}{6}l$

It did say "magntitude" of the impulse, but that's a small issue!

 

[Nexus99]

It did say "magntitude" of the impulse, but that's a small issue!

That's true:
$|\vec{J_R}| = m\frac{\omega}{6}l$
I have a question, is the impulse completely directed along x axis?

 

[PeroK]

I have a question, is the impulse completely directed along x axis?

Well, if you think about the rod just hanging there, we have the balanced forces of gravity and the restraining force at the pivot. The forces are balanced, so there is no motion. But, why not say that both forces are providing an equal an opposite impulse over a given time period? If impulse is force by time then why not?

Forces, impulses, accelerations are all vectors so they may cancel out when you add them.

That said, the impulse in the x-direction is a spike (large force over a short time giving a finite well-defined impulse); the impulse in the y-direction tends to zero as the time of the collision tends to zero, so is not particulary relevant in this case.

Interesting?!

 

[Nexus99]

Well, if you think about the rod just hanging there, we have the balanced forces of gravity and the restraining force at the pivot. The forces are balanced, so there is no motion. But, why not say that both forces are providing an equal an opposite impulse over a given time period? If impulse is force by time then why not?

Forces, impulses, accelerations are all vectors so they may cancel out when you add them.

That said, the impulse in the x-direction is a spike (large force over a short time giving a finite well-defined impulse); the impulse in the y-direction tends to zero as the time of the collision tends to zero, so is not particulary relevant in this case.

Interesting?!

Ok understood, this happens because internal the restraining force is impulsive during the collision, right?

 

[PeroK]

Ok understood, this happens because internal the restraining force is impulsive during the collision, right?

The reason there is an impulse is that the impact with the ball tries to rotate the rod about some point below the pivot. The pivot prevents this and provides an opposite torque, which is also the external force that reduces the linear momentum of the system. Angular momentum about the pivot, of course, is conserved.

 

[PeroK]

PS I assumed they are talking about the impulse from the pivot during the collision only.