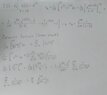goohu
- 53
- 3
Hello good folks!
I'm stuck trying to solve the problem b). In the theory book examples they are skipping steps and shortly states 'use algebra' and parsevals theorem to rewrite the Fourier series into the answer that is given.
So I've tried to use parsevals theorem but I still can't rewrite the result into the sum we are looking for.
View attachment 9282
In case the picture is too blurry;
a)
f(t) = $$\frac{{pi}^{2}}{3} + \sum_{k=1}^{\infty} \frac{4*{-1}^{k}}{{k}^{2}} cos(kt)$$
b) Calculate the sum of $$\sum_{k=1}^{\infty} \frac{{-1}^{k+1}}{{k}^{2}}$$
I'm stuck trying to solve the problem b). In the theory book examples they are skipping steps and shortly states 'use algebra' and parsevals theorem to rewrite the Fourier series into the answer that is given.
So I've tried to use parsevals theorem but I still can't rewrite the result into the sum we are looking for.
View attachment 9282
In case the picture is too blurry;
a)
f(t) = $$\frac{{pi}^{2}}{3} + \sum_{k=1}^{\infty} \frac{4*{-1}^{k}}{{k}^{2}} cos(kt)$$
b) Calculate the sum of $$\sum_{k=1}^{\infty} \frac{{-1}^{k+1}}{{k}^{2}}$$
Attachments
Last edited: