Discussion Overview
The discussion revolves around solving a continuous beam problem using the Castigliano method, focusing on finding the reactions in the beam under a distributed load. Participants explore the application of energy principles and the necessary equations to derive the solution.
Discussion Character
- Homework-related
- Mathematical reasoning
- Technical explanation
Main Points Raised
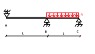
- The problem involves a continuous beam ABC with reactions at three supports (Ra, Rb, Rc) and a distributed load q.
- Initial equations for force and moment balances are proposed, but inconsistencies in sign conventions are noted by participants.
- Participants discuss the integration of the moment squared to find energy, with one expressing difficulty in performing the integration over the specified intervals.
- A formula for energy in terms of force is introduced, prompting questions about its derivation and application.
- Clarifications on the differentiation of moment squared with respect to force are provided, with references to the chain rule in calculus.
- One participant expresses confusion about the notation and the meaning of Mf(x) in the context of the discussion.
Areas of Agreement / Disagreement
Participants generally agree on the need to apply the Castigliano method and the relevant equations, but there are disagreements regarding sign conventions and the interpretation of certain terms. The discussion remains unresolved as participants work through the complexities of the problem.
Contextual Notes
There are limitations in the clarity of notation and assumptions regarding the definitions of variables, particularly in the context of differentiation and integration. Some participants express uncertainty about the integration process and the application of the formulas discussed.