- #1
Zouatine
- 22
- 0
hello everyone
1. Homework Statement
Problem:
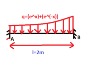
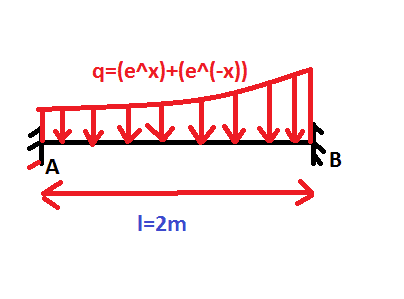
An AB beam, loaded with a distributed load q (KN/m), the length of the beam is 2 m.
EI=constant
find the reactions in the beam ,we use y''=-(1/EI) *M(x)
y''=-(1/EI) *M(x)[/B]
first we have 6 reactions (Va,Ha,Ma,Vb,Hb,Mb) in the supports.
∑F/x=0→ Ha+Hb=0 , Ha=-Hb=0 -------------1
∑F/y=0→ Va+Vb-Q=0 → Va+Vb=Q→ Va+Vb=∫ ((e^x)+(e^-x))dx 0≤ x ≤2
Va+Vb= 7,25 KN -------------2
∑M/b=0 → 2*Va- Q*(center of gravity of the load q)-Ma+Mb=0
center of gravity of the load q = (∫∫x*ds)/(∫∫ds)
∫∫x*ds= ∫∫x*dx*dy 0≤y≤(e^x)+(e^-x) , 0≤x≤2
∫∫x*ds= ∫∫x*dx*dy = 9,25 KN*m
∫∫ds= 7,25 KN
center of gravity of the load q = (∫∫x*ds)/(∫∫ds)=1,28 m (2-1,28)= 0,72m
2*Va- Q*0,72-Ma+Mb=0
2*Va-Ma+Mb=5,22 KN m----------3
Differential equation:
y''=-(1/EI) *M(x)
M(x) = ?? 0≤x<2
my problem is how to find the moment equation?
thanx
1. Homework Statement
Problem:
An AB beam, loaded with a distributed load q (KN/m), the length of the beam is 2 m.
EI=constant
find the reactions in the beam ,we use y''=-(1/EI) *M(x)
Homework Equations
y''=-(1/EI) *M(x)[/B]
The Attempt at a Solution
first we have 6 reactions (Va,Ha,Ma,Vb,Hb,Mb) in the supports.
∑F/x=0→ Ha+Hb=0 , Ha=-Hb=0 -------------1
∑F/y=0→ Va+Vb-Q=0 → Va+Vb=Q→ Va+Vb=∫ ((e^x)+(e^-x))dx 0≤ x ≤2
Va+Vb= 7,25 KN -------------2
∑M/b=0 → 2*Va- Q*(center of gravity of the load q)-Ma+Mb=0
center of gravity of the load q = (∫∫x*ds)/(∫∫ds)
∫∫x*ds= ∫∫x*dx*dy 0≤y≤(e^x)+(e^-x) , 0≤x≤2
∫∫x*ds= ∫∫x*dx*dy = 9,25 KN*m
∫∫ds= 7,25 KN
center of gravity of the load q = (∫∫x*ds)/(∫∫ds)=1,28 m (2-1,28)= 0,72m
2*Va- Q*0,72-Ma+Mb=0
2*Va-Ma+Mb=5,22 KN m----------3
Differential equation:
y''=-(1/EI) *M(x)
M(x) = ?? 0≤x<2
my problem is how to find the moment equation?
thanx