Solve Complex Integration: Find 2.36 Area of y=-x/2e+1/e+e & y=e^x/2

[minimoocha]

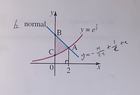
The area of two lines that I need to find is 2.36, however i need this in exact form. The lines are y=-x/2e+1/e+e the other line is y=e^x/2
Since y=-x/2e+1/e+e is on top it is the first function.
A=(the lower boundary is 0 and the top is 2) -x/2e+1/e+e-e^x/2

If you could please help!

 

[MarkFL]

Hello, and welcome to MHB! :)

I am assuming the linear function is:

$$f(x)=-\frac{x}{2e}+\frac{1}{e}+e$$

And the exponential function is:

$$g(x)=\frac{e^x}{2}$$

Are those correct?

 

[minimoocha]

Hello, and welcome to MHB! :)

I am assuming the linear function is:

$$f(x)=-\frac{x}{2e}+\frac{1}{e}+e$$

And the exponential function is:

$$g(x)=\frac{e^x}{2}$$

Are those correct?

[DESMOS]{"version":7,"graph":{"viewport":{"xmin":-10,"ymin":-12.5,"xmax":10,"ymax":12.5}},"randomSeed":"61268199dd3570cc9c59f2ef62b0245a","expressions":{"list":[{"type":"expression","id":"1","color":"#c74440","latex":"y=e^{\\frac{x}{2}}"},{"type":"expression","id":"3","color":"#388c46","latex":"y=-\\frac{x}{2e}+\\frac{1}{e}+e"}]}}[/DESMOS]

I am trying to find the area created by those two lines, however I can't integrate this, thank you for responding and for the welcome :D

 

[MarkFL]

Okay, so my assumptions were correct. So we wish to find this area (given that \(0\le x\le2\)):

So, we need to find the \(x\)-coordinate of the point of intersection. Hence, we need to solve:

$$-\frac{x}{2e}+\frac{1}{e}+e=\frac{e^x}{2}$$

We cannot get a solution in terms of elementary functions, and in fact we find:

$$x=-W\left(e^{3+2e^2}\right)+2+2e^2$$

Where \(W\) is the product log function. Using a numeric root finding technique, we find:

$$x\approx1.7124201115416355473$$

And so the area would be approximately given by:

$$A\approx\int_0^{1.7124201115416355473} -\frac{x}{2e}+\frac{1}{e}+e-\frac{e^x}{2}\,dx+\int_{1.7124201115416355473}^2 \frac{e^x}{2}-\left(-\frac{x}{2e}+\frac{1}{e}+e\right)\,dx$$

Can you proceed?

 

[minimoocha]

Okay, so my assumptions were correct. So we wish to find this area (given that \(0\le x\le2\)):

View attachment 9785

So, we need to find the \(x\)-coordinate of the point of intersection. Hence, we need to solve:

$$-\frac{x}{2e}+\frac{1}{e}+e=\frac{e^x}{2}$$

We cannot get a solution in terms of elementary functions, and in fact we find:

$$x=-W\left(e^{3+2e^2}\right)+2+2e^2$$

Where \(W\) is the product log function. Using a numeric root finding technique, we find:

$$x\approx1.7124201115416355473$$

And so the area would be approximately given by:

$$A\approx\int_0^{1.7124201115416355473} -\frac{x}{2e}+\frac{1}{e}+e-\frac{e^x}{2}\,dx+\int_{1.7124201115416355473}^2 \frac{e^x}{2}-\left(-\frac{x}{2e}+\frac{1}{e}+e\right)\,dx$$

Can you proceed?

Actually, because I do not do very hard maths, it is just 0<x<2
That is wayyy to complicated for me to understand. Desmos deformed it because my graphing calculator says different.
What I am doing is for my maths assignment:

So I had to find the equation of the normal for the point (2,e)
Which was = to the eq of the line y=-\frac{x}{2e}+\frac{1}{e}+e
So I need to find the area of e^x/2 and - from the normal
Which hopefully i am right would = to normal-curve = the area of the weird triangle, because i need it on exact form.

The original question is: The diagram shows part of the curve with the equation y=e^x/2. Find the exact area bound by the curve and the lines AB and BC.
THANK YOU THOUGH! I APPRECIATE IT A LOT!

 

[MarkFL]

Okay, this is a different problem. I didn't notice the difference between my assumptions and the functions you have in the live calculator above. Sorry for the confusion.

We are given the curve:

$$y=e^{\frac{x}{2}}$$

Let's find the derivative:

$$\frac{dy}{dx}=\frac{1}{2}e^{\frac{x}{2}}[$$

And so the slope of the normal line is:

$$m=\left.-\frac{dx}{dy}\right|_{x=2}=-\frac{2}{e}$$

And so the normal line is given by:

$$y=-\frac{2}{e}(x-2)+e$$

And thus, the shaded area is given by:

$$A=\int_0^2 -\frac{2}{e}(x-2)+e-e^{\frac{x}{2}}\,dx$$

Let's clean that up a bit:

$$A=\int_0^2 -\frac{2}{e}x+\frac{e^2+4}{e}-e^{\frac{x}{2}}\,dx$$

So, our integrand has 3 types of expressions...one with \(x\) to the first power, a constant, and an exponential. Do you have any thoughts on how to find the anti-derivative?

 

[minimoocha]

yes.
$$$$ A=[-x^2e+ ((e^3+4x)/e^2))-1/2e^-0.5x]

I think?

 

[MarkFL]

I find:

$$A=\int_0^2 -\frac{2}{e}x+\frac{e^2+4}{e}-e^{\frac{x}{2}}\,dx=\left[-\frac{1}{e}x^2+\frac{e^2+4}{e}x-2e^{\frac{x}{2}}\right]_0^2$$

Do you see that if you differentiate the anti-derivative within the brackets, you get the integrand? I used the power rule and the rule for exponential functions to get it.

Can you proceed?

 

[minimoocha]

that makes much more sense- I can proceed :)
\[ A=((-1/e)2^2+(2^2+4/e)2-2e^2/2)-((-1/e)0^2+(0^2+4/4)(0)-2e^0/2)) \]
which simplifies to
\[ A=((-1/e)(4))+((8/e)(2)-2e^1)-(2e^0) \]
this is as far as i got :)
\( A=((-1/e)(4))+((8/e)(2)-2e)-(2) \)

 

[MarkFL]

You are making some mistakes in your application of the FTOC.

$$A=\left(-\frac{1}{e}2^2+\frac{e^2+4}{e}2-2e^{\frac{2}{2}}\right)-\left(-\frac{1}{e}0^2+\frac{e^2+4}{e}0-2e^{\frac{0}{2}}\right)$$

$$A=-\frac{4}{e}+\frac{2e^2+8}{e}-2e+2=\frac{2(e+2)}{e}$$

 

[minimoocha]

You are making some mistakes in your application of the FTOC.

$$A=\left(-\frac{1}{e}2^2+\frac{e^2+4}{e}2-2e^{\frac{2}{2}}\right)-\left(-\frac{1}{e}0^2+\frac{e^2+4}{e}0-2e^{\frac{0}{2}}\right)$$

$$A=-\frac{4}{e}+\frac{2e^2+8}{e}-2e+2=\frac{2(e+2)}{e}$$

Sorry I've been staring at maths all day. Thank you so much for the help! You are a lifesaver!