Solve Fermi-Dirac Integral: Get Help Now!

[arneet]

i am completely lost. there is an integral in my textbook in fermi dirac statistics whose result is written directly and am not able to understand . it is

.
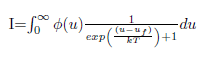on expansion by using the method of taylor's series the result should be

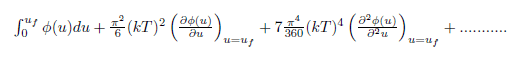
where u_f is such that function of u is zero for u greater than uf.
please reply as soon as possible. thanks.

 

[Alpharup]

I think this should have been posted in physics thread. Anyways, i will explain here...Assume u is greater than uf...so (u-uf) is so large...
so in 1+(exp(u-uf)/kT) can be approximated as (exp(u-uf)/kT)

The reciprocal of this term is (exp-(u-uf)/kT).

Hope this helps

 

[arneet]

I think this should have been posted in physics thread. Anyways, i will explain here...Assume u is greater than uf...so (u-uf) is so large...
so in 1+(exp(u-uf)/kT) can be approximated as (exp(u-uf)/kT)

The reciprocal of this term is (exp-(u-uf)/kT).

Hope this helps

thanks for replying,it helped.