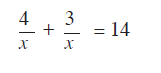SUMMARY
The discussion focuses on solving the equation $$\frac{7}{x}=14$$ to find the value of x in the denominator. The correct steps involve dividing both sides by 7, resulting in $$\frac{1}{x}=2$$, and then inverting both sides to conclude that $$x=\frac{1}{2}$$. The method of cross-multiplication is mentioned but is not applicable in this context, as the equation involves a simple division rather than addition. The solution is confirmed as correct by multiple participants.
PREREQUISITES
- Understanding of basic algebraic operations
- Familiarity with fractions and denominators
- Knowledge of cross-multiplication techniques
- Ability to manipulate equations to isolate variables
NEXT STEPS
- Study the principles of solving rational equations
- Learn about cross-multiplication and its applications
- Explore methods for simplifying fractions
- Practice isolating variables in various algebraic equations
USEFUL FOR
Students learning algebra, educators teaching mathematical concepts, and anyone seeking to improve their problem-solving skills in rational equations.