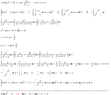SUMMARY
The integral of ln(x²-1) can be solved using integration by parts and partial fraction decomposition. The correct approach involves recognizing that ln(x²-1) can be expressed as ln(x-1) + ln(x+1) only under certain conditions, specifically for x > 1. The final solution is given by xln(x²-1) - 2x - ln|x-1| + ln|x+1| + C. Key mistakes in earlier attempts included incorrect application of logarithmic properties and errors in partial fraction decomposition.
PREREQUISITES
- Understanding of integration techniques, specifically integration by parts.
- Familiarity with logarithmic properties and their domains.
- Knowledge of partial fraction decomposition methods.
- Ability to perform polynomial long division.
NEXT STEPS
- Study the application of integration by parts in solving integrals.
- Learn about the properties and domains of logarithmic functions.
- Research techniques for partial fraction decomposition in calculus.
- Practice polynomial long division to reinforce understanding of algebraic manipulation.
USEFUL FOR
Students and educators in calculus, mathematicians solving integrals, and anyone looking to deepen their understanding of logarithmic integration techniques.