Solve Modified Atwood Problem: Find T1, T2, T3, T4, T5 & F

[go2cnavy]

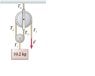
Q: A 10.2 Kg block is held in place by a massless rope passing over two massless, frictionless pulleys. Find the tensions T1, T2, T3, T4, T5 and the magitude of force F. Please see attached file for picture.

I know:

T1=mg=99.96N

My question, since the system is in equilibrium, shouldn't T2=T3=T5? IN addition, wouldn't T4 be equal but opposite to T3? I just get confused on how to set up the system of equations. Please help.

 

[Doc Al]

My question, since the system is in equilibrium, shouldn't T2=T3=T5?

This is true because the rope is massless and the pulleys are frictionless, not because the system is in equilibrium. Under these conditions, the tension is uniform throughout that piece of rope.

IN addition, wouldn't T4 be equal but opposite to T3?

Why do you think that? Consider the top pulley: What forces pull up on it? What forces pull down?

 

[go2cnavy]

I had to see it for myself in a real world application. Today I set up the pulleys at physics lab and used a 200 gram mass as the hanging weight.

This gives my T1=mg=1.96 N.

The amount of force F required to keep the system static was .8N measured with a spring scale.

In addition, the pulley system was alos hanging from a spring scale and the tension at T4 was @ the sum of the pulley weights+T1+F.

If I let T1 = mg=(10.2)(-9.8)=-99.96N, Then is it safe to conclude that
T2+T3=99.96N so T2 and T3 each = 49.98N

 

[Doc Al]

Sounds like you've got it.

 

[go2cnavy]

Thank you! I just found this site and will be here often now. Please check my work...

mg=99.98N
T1=99.96N
T2=49.98N
T3=49.98N
T4=-(mg+F)=149.94N
T5=49.98N
F=-49.98N

 

[Doc Al]

Looks good. Two nitpicks: (1) Just give the magnitudes of the forces, forget the signs. (Tension in a rope is always positive.) (2) Round off to a reasonable number of significant figures. (Your results are not accurate to 4 digits!)

 

[go2cnavy]

Thank you for the help and the advice. Much appreciated!