SpectraPhy09
- 23
- 3
- Homework Statement
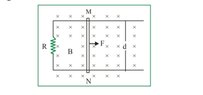
- Two long Horizontal rails, a distance d apart and each having a resistanc λ per unit length are joined one end by a resistance R. A perfectly conducting rod MN of mass m is free to slide along the rails without friction v(I have attached the file for the diagram plz check) . There is a uniform magnetic field of induction B Normal to the plane of the paper and directed into the paper. Variable Force F is applied to the rod MN such that, as the rod moves, a constant current i and flows through R.
(i) Find the applied force F as function of distance x of the rod from R.
- Relevant Equations
- Force due to a current carrying wire = iBl
Where i = current
B = Magnetic field
L = length of the wire
E.M.F induced due to a rod of length l moving with Velocity V in Magnetic field B = VBl
Its applicable only when V, B and I are mutually perpendicular to each other
I request please go through my solution
Total Resistance = R + 2λx
V(ind) = vBd
I(ind)= vBd/(R + 2λx )
v = i(R + 2λx )/Bd
If force on the wire due to induced current is iBl then
Fnet = iBd - F ...(i)
or Fnet = F - iBd ...(ii)
Fnet = v(dv/dx)
v(dv/dx) = iBd - F
By solving we get
Fnet by (i) is iBd - 2λi²m(R+2λx)/B²d²
(ii)is 2λi²m(R+2λx)/B²d² - iBd
Which one of this is correct ? Or both are correct ? Did I made any mistake in the solution
Total Resistance = R + 2λx
V(ind) = vBd
I(ind)= vBd/(R + 2λx )
v = i(R + 2λx )/Bd
If force on the wire due to induced current is iBl then
Fnet = iBd - F ...(i)
or Fnet = F - iBd ...(ii)
Fnet = v(dv/dx)
v(dv/dx) = iBd - F
By solving we get
Fnet by (i) is iBd - 2λi²m(R+2λx)/B²d²
(ii)is 2λi²m(R+2λx)/B²d² - iBd
Which one of this is correct ? Or both are correct ? Did I made any mistake in the solution
 ##\qquad## !
##\qquad## !