Solve Parallelogram: Lengths X & Y, Angle Z, A=15in, B=20.5in

  • Context: MHB 
  • Thread starter Thread starter Storminnorman
  • Start date Start date
  • Tags Tags
    Parallelogram
Click For Summary
SUMMARY

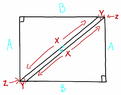
The discussion focuses on solving for the lengths X and Y and angle Z of a parallelogram situated within a rectangle measuring 15 inches in height and 20.5 inches in width. The area of the parallelogram is expressed as A_P = 1.5X, while the relationship between the rectangle's dimensions and the parallelogram is established through the equation AB = (B - Y)A + 1.5X. Utilizing Pythagorean theorem, the equation B - Y = √(X² - A²) is derived, leading to a single-variable equation for further analysis.

PREREQUISITES
  • Understanding of basic geometry concepts, specifically parallelograms and rectangles.
  • Familiarity with the Pythagorean theorem and its application in solving for unknown lengths.
  • Ability to manipulate algebraic equations to isolate variables.
  • Knowledge of area calculations for geometric shapes.
NEXT STEPS
  • Study the properties of parallelograms and their relationship to rectangles.
  • Learn how to apply the Pythagorean theorem in various geometric contexts.
  • Explore algebraic techniques for solving equations with one variable.
  • Investigate area formulas for different geometric shapes, including triangles and parallelograms.
USEFUL FOR

Students, educators, and professionals in mathematics or engineering fields who require a deeper understanding of geometric relationships and algebraic problem-solving techniques.

Storminnorman
Messages
1
Reaction score
0
A parallelogram exists within a rectangle which measures 15 inches tall by 20.5 inches wide.

A=15 inches
B=20.5 inches
C=1.5 inches
(C makes a 90° angle with X)

Solve for lengths X and Y and angle Z of the parallelogram and please tell me how you did it!

View attachment 5171
 

Attachments

  • Screenshot_2016-01-18-19-33-32-1-1.png
    Screenshot_2016-01-18-19-33-32-1-1.png
    30.6 KB · Views: 119
Mathematics news on Phys.org
Hello and welcome to MHB, Storminnorman! :D

We ask that our users show their progress (work thus far or thoughts on how to begin) when posting questions. This way our helpers can see where you are stuck or may be going astray and will be able to post the best help possible without potentially making a suggestion which you have already tried, which would waste your time and that of the helper.

I think the way I would begin is to observe that the area of the parallelogram is:

$$A_P=1.5X$$

And then we can deconstruct the area of the rectangle into 2 right triangles and the parallelogram:

$$AB=(B-Y)A+1.5X$$

Now, by Pythagoras, we find:

$$B-Y=\sqrt{X^2-A^2}$$

Hence:

$$AB=A\sqrt{X^2-A^2}+1.5X$$

Now you have an equation with only one unknown...can you proceed?
 

Similar threads

MHB Find Length of Side in Right Triangle w/ 45°, 90°, and 45° Angle
  • · Replies 2 ·
Replies
2
Views
2K
MHB Solving for $x+y$ in $\triangle ABC$
  • · Replies 3 ·
Replies
3
Views
1K
MHB Solving System of Equalities: x^2-y\sqrt xy & y^2-x\sqrt xy =3
  • · Replies 2 ·
Replies
2
Views
1K
MHB Solve System of Equalities: x^2+xy+y^2, x^2+xz+z^2, y^2+yz+z^2
  • · Replies 7 ·
Replies
7
Views
2K
MHB Find value of x and area of parallelogram: a,b,c,P
  • · Replies 2 ·
Replies
2
Views
2K
MHB Calculating Triangle Side Length with Known Angles and Radius
  • · Replies 2 ·
Replies
2
Views
2K
MHB Solve System of 4 Equalities: x+y+z+w=22, xyzw=648
  • · Replies 6 ·
Replies
6
Views
2K
MHB Is the Inequality $(a+b+c)^2+(x+y+z)^2≥1$ Always True?
  • · Replies 4 ·
Replies
4
Views
2K
MHB Inequality c≤√[(x−a^2+(y−b)^2+(z−c)^2]+√(x2+y2+z2)
  • · Replies 5 ·
Replies
5
Views
2K
MHB Finding the Leg Lengths of a Right Triangle with an Acute Angle of 22°
  • · Replies 2 ·
Replies
2
Views
1K