prettybabylily
- 4
- 0
Can anyone help me solve this problem that i am a little confused about? i think the answer is tension=mgsin"theta", am i close at all?!
thanks!
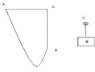
According to the picture, from point A to point B is a string that is attached to wall. The string is twice the distance from Point A to Point O, and Point A to Point O's distance is the same as the distance between Point B Point O. If i put k upto the string, which has a box M that is attached to it. when it stops rolling on the string. what is the Tension on the string? (no friction applied)
thanks!
According to the picture, from point A to point B is a string that is attached to wall. The string is twice the distance from Point A to Point O, and Point A to Point O's distance is the same as the distance between Point B Point O. If i put k upto the string, which has a box M that is attached to it. when it stops rolling on the string. what is the Tension on the string? (no friction applied)