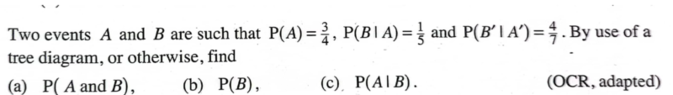chwala
Gold Member
- 2,828
- 420
- Homework Statement
- See attached
- Relevant Equations
- Probability
I would like to know how one can use the tree diagram...hence my post... otherwise, i was able to solve problem as follows,
a. ##P(A∩B)= \dfrac{3}{4} ×\dfrac{1}{5}=\dfrac{3}{20}##
b. ## P(B/A')=\dfrac{P(B)-\dfrac{3}{20}}{P(A')}##
##\dfrac{3}{7}=\dfrac{P(B)-\dfrac{3}{20}}{\dfrac{1}{4}}##
...
##P(B)=\dfrac{9}{35}##
c. ## P(A/B)=\dfrac{3}{20} ×\dfrac{35}{9}=\dfrac{7}{12}##