Solve Word Problem: Find Rectangle Dimensions from Circular Piece of Sheet Metal

[powp]

Hello All

I have this word problem that I am having problems with

Here it is

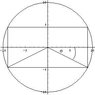
A circular piece of sheet metal has a diameter of 20 in. The edges are to be cut off to form a rectangle of area in^2. What are dimensions of the rectangle??

Here is what I have figured out. Not sure if it of any use

Formula of Circle is

10^2 = y ^ 2 + x ^ 2

Area of rectangle

160 = LW

Not sure how to go from here. Please help

Thanks

 

[saltydog]

A circular piece of sheet metal has a diameter of 20 in. The edges are to be cut off to form a rectangle of area in^2. What are dimensions of the rectangle??

Here is what I have figured out. Not sure if it of any use

Formula of Circle is

10^2 = y ^ 2 + x ^ 2

Area of rectangle

160 = LW

Not sure how to go from here. Please help

Thanks

So, as I see it you have a circle of radius 10 and want to draw a rectangle in it with a total area of 160 right? Look at the plot below (drawn to scale) and where I have theta. Can you figure out what the length and height has to be using some trig expressions?

 

[powp]

Don't think I have enough info to use trig expessions. All I know for that triangle is the hypotenuse is 10 in and is a right angle triangle.

How can I determine the remaining info?
if I use sin I need opposite side?

 

[plucker_08]

IT’S ALL GEOMETRY…

X^2 + Y^2 = 20^2 = 400 ----------------------DIAGONAL OF THE RECTANGLE

XY = 160
2XY = 320

X^2 + 2XY + Y^2 = 400 + 320 = 720
(X+Y) ^2= 720


X+Y = 12 √5


X^2 – 2XY + Y^2 = 400 – 320 = 80
(X-Y)^ 2 = 80

X-Y = 4 √5

2 EQS., 2 UNKNOWNS

2X = 4 √5 + 12 √5 = 16 √5


X = 8 √5
Y = 4√5

 

[MaxwellPhill]

Nice explanation plucker.

 

[powp]

thanks why did you multiply xy = 160 by 2 ??

 

[plucker_08]

adding 2xy to x^2 + y^2 will yield to an expression x^2 + 2xy + y^2 which is the square of the sum of the sides of the rectangle...(x + y)

subtracting 2xy to x^2 + y^2 will yield to an expression x^2 - 2xy + y^2 which is the square of the difference of the sides of the rectangle...(x - y)

you will have 2 eqs and 2 unknows...

 

[powp]

how can you just add values to the equation?? How do you know when to do this?

 

[saltydog]

Hey Powp. Sorry for not get getting back with you last night but looks like these guys helped you ok. Yea, I didnt' see the obvious algegra:

x^2+y^2=400

xy=160

Solving for x or y in the second equation and substituting into the first leads to the same equation for both x and y:

r^4-400r^2+160^2=0

Now, using the quadratic formula, just figure out which of the 4 roots make sense.

I drew a pretty graph though.