Solving a FRAMEwork Static Problem - Find Correct Solution

Click For Summary

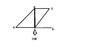
Discussion Overview

The discussion revolves around solving a static framework problem involving forces in a truss structure. Participants explore various approaches to calculating forces at different joints, addressing concepts related to support types, equilibrium equations, and the nature of zero force members.

Discussion Character

  • Technical explanation
  • Mathematical reasoning
  • Debate/contested
  • Homework-related

Main Points Raised

  • Some participants propose two different approaches to calculating forces at supports C and D, with one method yielding Dy = -20N and the other suggesting Cx = Dx.
  • One participant expresses confusion about the direction of forces at roller supports, questioning whether the force always opposes the applied load.
  • Another participant clarifies that the roller must rest against a wall for stability, indicating that earlier assumptions about force directions were incorrect.
  • Participants discuss the calculations for various joints, with some values being confirmed as correct while others are challenged, particularly regarding the direction of forces and the identification of tension versus compression.
  • There is a debate about the concept of zero force members, with one participant asserting that these members cannot carry load, while another argues that their presence does not affect stability in the current loading scenario.
  • One participant reports a significant discrepancy between lab results and theoretical calculations, prompting further inquiry into the reasons behind this difference.

Areas of Agreement / Disagreement

Participants do not reach a consensus on the correctness of certain calculations, particularly regarding the forces at joint C and the nature of zero force members. Multiple competing views remain on the interpretation of roller support forces and the implications of zero force members.

Contextual Notes

Limitations include unresolved assumptions about force directions, the dependence on specific loading conditions, and the potential for errors in sign usage in equilibrium equations.

stupif
Messages
99
Reaction score
1
1. every member is 0.45m and all the angle is 45degree...
C is fixed support, D is roller support









3. Ʃfx = 0 , Cx = 0
Ʃfy = 0 , Cy + Dy = 20N

ƩMc = 0 , 20(0.45) + Dy(0.45) = 0
Dy = -20N


OR
Ʃfx = 0 , Cx - Dx = 0
Cx = Dx
Ʃfy = 0, Cy -20N = 0
Cy = 20N
ƩMc = 0 , 20(0.45) + Dx(0.45) = 0
Dx= -20N

may i know which one is correct??
help me...please...
 

Attachments

  • Untitled11.png
    Untitled11.png
    4 KB · Views: 505
Physics news on Phys.org
The second one is correct.

I think you meant to say that C is pinned (it can take forces in the x and y directions), and that D is a roller support (it can only take a load in one direction at a right angle to the rollers (in the negative x direction in this case)).
 
i don't understand about roller support there...
how to know the force is in which direction?
i thought the roller support 's force is always oppose to the force applied(20N)...
thank you
 
stupif said:
i don't understand about roller support there...
how to know the force is in which direction?
i thought the roller support 's force is always oppose to the force applied(20N)...
thank you
No, not always, and this problem is an example: the roller must rest on the side wall, not the floor; otherwise, the frame would be unstable, since there would be no way to balance the horizontal force at the other support. When you assumed this in your first incorrect solution, you made an error when summing moments about C: You said
ƩMc = 0 , 20(0.45) + Dy(0.45) = 0
, but a Dy force cannot produce a moment about C (there is no moment arm) , so your equation should have said
ƩMc = 0 , 20(0.45) + Dy(0) = 0
, which is nonsensical, and therefore incorrect.
 
ok...i got it...thank you

now these are my answer...could you help me check and are they correct?

C joint
(vertical)
Cy - Fce sin45 = 0
20 - Fce sin 45= 0
Fce = 28.28N

(horizontal)
Cx + Fbc - Fce cos 45 = 0
-20 + Fbc - 28.28cos 45 = 0
Fbc= 40N

joint D(horizontal)
Dx = Fde
Fde = -20N

joint E(horizontal)
Fde + Fce cos45 -Fae = 0
-20 + 28.28cos45 - Fae = 0
Fae = 0

(vertical)
Fbe + Fce cos45 -20 = 0
Fbe = 0

joint A
Fab =0

i know they are wrong...but i don't know which one is wrong and how come will be wrong...help me...i'm lost in statics! thanks
 
stupif said:
ok...i got it...thank you

now these are my answer...could you help me check and are they correct?

C joint
(vertical)
Cy - Fce sin45 = 0
20 - Fce sin 45= 0
Fce = 28.28N
Yes, this value is correct, good work, but you must also indicate whether it is tension force or compression force. Member tension forces always pull away from the joints on which they act, and member compression forces always push toward the joint on which they act.
(horizontal)
Cx + Fbc - Fce cos 45 = 0
-20 + Fbc - 28.28cos 45 = 0
Fbc= 40N
No, this is not correct. You have to be very careful of force and force reaction directions and the use of the plus and minus sign. Which way does Cx reaction force on the joint point, to the left or right, and is it thus plus or minus? You can sum moments about D to get its direction.
joint D(horizontal)
Dx = Fde
Fde = -20N
Yes, tension or compression?
joint E(horizontal)
Fde + Fce cos45 -Fae = 0
-20 + 28.28cos45 - Fae = 0
Fae = 0
excellent, now you are cookin'
(vertical)
Fbe + Fce cos45 -20 = 0
Fbe = 0
Yeahhh, buddy!:smile:
joint A
Fab =0
Yes, again!
i know they are wrong...but i don't know which one is wrong and how come will be wrong...help me...i'm lost in statics! thanks
Actually, you did yourself proud...the only errors are whether the forces are T or C, and the force in BC was wrong. Try that one again.
 
PhanthomJay said:
Yes, this value is correct, good work, but you must also indicate whether it is tension force or compression force. Member tension forces always pull away from the joints on which they act, and member compression forces always push toward the joint on which they act.
No, this is not correct. You have to be very careful of force and force reaction directions and the use of the plus and minus sign. Which way does Cx reaction force on the joint point, to the left or right, and is it thus plus or minus? You can sum moments about D to get its direction. Yes, tension or compression? excellent, now you are cookin' Yeahhh, buddy!:smile: Yes, again! Actually, you did yourself proud...the only errors are whether the forces are T or C, and the force in BC was wrong. Try that one again.
thank you...

Fbc = 20N??

Fbc = Fce cos 45
Fbc = 20N

but why just now what i did is wrong? i feel like is correct because
Fx = 0
Fx contain Cx, Fbc, Fce cos 45, that's why i formed a equation.Fab = tension
Fae= tension
Fbe = compression
Fde= compression
Fce= tension
Fbc = compression
 
stupif said:
thank you...

Fbc = 20N??

Fbc = Fce cos 45
Fbc = 20N

but why just now what i did is wrong? i feel like is correct because
Fx = 0
Fx contain Cx, Fbc, Fce cos 45, that's why i formed a equation.
Yes, but you formed it wrong. You wrote:
C joint

(horizontal)
Cx + Fbc - Fce cos 45 = 0
-20 + Fbc - 28.28cos 45 = 0
Fbc= 40N
When you should have wrote, per my earlier hint on signage
C_x + F_{bc} - F_{ce} cos 45 = 0
+20[/color] + F_{bc} - F_{ce} cos 45 = 0
Now solve for F_bc. The plus and minus sign will bite you every time if you let it. Do you see your error?
Fab = tension
Fae= tension
Fbe = compression
but these you have identified as all zero force members, neither in tension nor compression
Fde= compression
Yes!
Fce= tension
Yes!
Fbc = compression
NO!

You only got 2 out of 6 correct :frown::smile:
(I need to work on my LateX)
 
Fbc should be tension...i see it...

my understanding about zero force members...

zero force members are a member which cannot carry load. hence there is no force in these members. these members do not have compression force and tension force.
the existence of zero force members are to stabilise other members.

my understanding is correct or no?
 
  • #10
stupif said:
Fbc should be tension...i see it...
NO, that it is not right. Did you work out the equation?
+20 + F_{bc} - F_{ce} cos 45 = 0
+ 20 + F_{bc} - 20 = 0
F_{bc} = ____?___
my understanding about zero force members...

zero force members are a member which cannot carry load. hence there is no force in these members. these members do not have compression force and tension force.
the existence of zero force members are to stabilise other members.

my understanding is correct or no?
Not quite. The zero force members in this problem are not stabilizing anything. You can take them out of the frame as if they didn't exist, and it doesn't change the solution or stability in any way.
 
  • #11
Fbc = 0N??
is not tension and compression...

then why this phenomenon happenned? i mean zero force members...
 
  • #12
stupif said:
Fbc = 0N??
is not tension and compression...

then why this phenomenon happenned? i mean zero force members...
They only have no force in them because of the way the truss is loaded with only a force appied at E...If a load was applied downward at A, all the members would have forces in them. In other words, for the given problem and loading, the members are not needed, they are just extras in case some day you wished to apply at load at A...right now, they just go along for a ride ...
 
  • #13
but when i doing this in lab, my result from lab is quite big difference to the theoretical result. the aim of the lab is to determine the forces in members and the model is same as the diagram. the force applied is also same. What is the possible source of errors?
Do we need to consider the weight of the members?
 
  • #14
stupif said:
but when i doing this in lab, my result from lab is quite big difference to the theoretical result. the aim of the lab is to determine the forces in members and the model is same as the diagram. the force applied is also same. What is the possible source of errors?
Do we need to consider the weight of the members?
My assumption was that the weight of the members could be neglected. However, if the member weights are significant (and they might be since you are only applying a 20N load), then yes, you would have to consider their weight. For the puposes of the calculation, you may assume each member's weight is distributed 1/2 to each of its end joints, and applied as a load at those joints.
 
  • #15
thank you very much...you help me a lot...appreciate your help...(bow)
 

Similar threads

Engineering Solve X-Forces for Frame Statics Problem
  • · Replies 5 ·
Replies
5
Views
2K
Finding the reactions at the supports, 3D model
  • · Replies 3 ·
Replies
3
Views
7K
How can I solve this structural mechanics problem accurately?
  • · Replies 5 ·
Replies
5
Views
3K
Finding Reaction Forces on Pin Supports in a Static Equilibrium System
  • · Replies 1 ·
Replies
1
Views
2K
Frame Question: Trouble Solving Structural Members
  • · Replies 9 ·
Replies
9
Views
2K
Finding Equilibrium Forces in a Two-Member Frame
  • · Replies 4 ·
Replies
4
Views
8K
How to Solve a 3-D Truss Problem: Finding Forces at a Specific Point
  • · Replies 1 ·
Replies
1
Views
2K
Analysis of Structures Homework: Find Forces on Member AD
  • · Replies 4 ·
Replies
4
Views
3K
Undergrad Mechanics question on vector statics
  • · Replies 3 ·
Replies
3
Views
4K
Virtual Work and Static Equilibrium
  • · Replies 3 ·
Replies
3
Views
2K