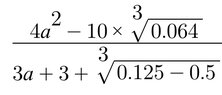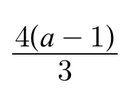Solving Cubic Root Algebra: Don't Know the Steps

  • Context: MHB 
  • Thread starter Thread starter STS
  • Start date Start date
  • Tags Tags
    Algebra Cubic Root
Click For Summary
SUMMARY

The discussion revolves around solving a cubic root algebra problem involving the expression $$\frac{4a^2-10\times\sqrt[3]{0.064}}{3a+3+\sqrt[3]{0.125}-0.5}.$$ Participants express confusion regarding the value of 'a', specifically that it should not be -1, and question the validity of the equation due to a potential typo. The correct evaluation of the cubic root is critical for arriving at the right answer.

PREREQUISITES
  • Understanding of cubic root operations
  • Familiarity with algebraic expressions and simplification
  • Knowledge of basic mathematical rules regarding variables
  • Ability to identify and correct typographical errors in equations
NEXT STEPS
  • Study the properties of cubic roots and their applications in algebra
  • Learn how to simplify complex algebraic expressions
  • Explore common algebraic mistakes and how to identify them
  • Practice solving equations involving variables and roots
USEFUL FOR

Students learning algebra, educators teaching mathematical concepts, and anyone seeking to improve their problem-solving skills in cubic root equations.

STS
Messages
5
Reaction score
0
I don't understand this.
a is not suppose to be -1; this is the only rule in the equation
The answer is the second picture, I just don't know the steps that lead to that answer.
View attachment 8926
 

Attachments

  • 9CF9CCB6-D594-44E5-8980-651A512FD6DD.jpeg
    9CF9CCB6-D594-44E5-8980-651A512FD6DD.jpeg
    9.5 KB · Views: 126
  • F124AFBD-F35E-4E44-81AF-3136409AF46D.jpeg
    F124AFBD-F35E-4E44-81AF-3136409AF46D.jpeg
    2.7 KB · Views: 115
Mathematics news on Phys.org
STS said:
I don't understand this.
a is not suppose to be -1; this is the only rule in the equation
The answer is the second picture, I just don't know the steps that lead to that answer.
In order for this to be correct we would need [math]\sqrt[3]{ 0.125 - 0.5 } = 0[/math], which clearly isn't true. Is there a typo?

-Dan
 
Hi STS.

You probably mean the following expression:
$$\frac{4a^2-10\times\sqrt[3]{0.064}}{3a+3+{\color{red}\sqrt[3]{0.125}}-0.5}.$$
 

Similar threads

High School What went wrong with (-x)^2=x^2?
  • · Replies 22 ·
Replies
22
Views
2K
MHB Understanding Cubic Equation Formula for Polynomials of Degree Three
  • · Replies 9 ·
Replies
9
Views
3K
Undergrad Does this make a cubic out of a quadratic system?
  • · Replies 9 ·
Replies
9
Views
2K
MHB Solving Cubic Equation: x^3 - kx + (k + 11) = 0
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Trouble Solving an Equation that has square roots on both sides
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Finding Solutions to a Cubic Equation with Multiple Roots
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad The solution to a cubic equation
  • · Replies 2 ·
Replies
2
Views
2K
MHB Solve the cubic equation 4u^3+3u−3=0
  • · Replies 2 ·
Replies
2
Views
2K
MHB Can Cubic Roots and Square Roots Combine to Equal One?
  • · Replies 5 ·
Replies
5
Views
2K
MHB Using Substitution to Solve Cubic Equations
  • · Replies 3 ·
Replies
3
Views
2K