Solving Differential Equation: Boy & Girl's Meeting Time

[GregoryGr]

Homework Statement

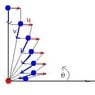
A boy is on a boat, at a distance H from the shore, when he sees a girl (at the point on the shore where the distance is measured) running with a constant velocity u parallel to the shore. At that time, he moves towards her, with a speed v, in such a way, that the point of the boat is always pointed at the girl (so his vector is always pointing her way). Find the time of their meeting.

Homework Equations

$$ \vec{v}= \frac{dr}{dt}\hat{r}+r\frac{d\theta}{dt}\hat{\theta} $$

The Attempt at a Solution

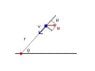
I changed the system of coordinates so the girl is stationary at O' , and using polar coordinates since the vector of the boat is always in the radial direction. The velocity for the boat in polar coordinates can be written:
$$ \vec{v}= -(v+ucos\theta)\hat{r}+vsin\theta\hat{\theta} $$

And since the 2 quantities in front of the singular vectors must be the same, I get 2 differential equations which give me this:

$$ \frac{dr}{r}= \frac{-(v-ucos\theta)d\theta}{usin\theta} $$


I am a noob at solving differentials, so firstly, are my equations right, and second, can somebody help me figure out how to do the math?

 

[haruspex]

are my equations right, and second, can somebody help me figure out how to do the math?

Yes, I agree with your first two equations, and I think the third is right. Once you have a solution you can check it satisfies the second one.
If you expand the numerator, the second term is easy to integrate. The first becomes the integral of a cosecant, which is standard enough that you can look it up. If you're interested in doing it from first principles, multiply top and bottom by sine and convert the sin² in the denominator to 1-cos². You can then factorise that and expand it using partial fractions. Each fraction is readily integrated.

 

[ehild]

I changed the system of coordinates so the girl is stationary at O' , and using polar coordinates since the vector of the boat is always in the radial direction. The velocity for the boat in polar coordinates can be written:
$$ \vec{v}= -(v+ucos\theta)\hat{r}+vsin\theta\hat{\theta} $$

I think there should be "u" instead of v in front of sinθ. Check.


ehild

 

[haruspex]

I think there should be "u" instead of v in front of sinθ. Check.


ehild

Yes, I saw that, but it must be a transcription error since it is correct in the later equation.

 

[ehild]

A figure would be necessary. I assume that the girl runs to the left so the boy has a horizontal velocity component u to the right. See figure. That component and the boy's radial velocity component v add up and determine the boy's next position.
You see that the horizontal component u makes r increase, but θ decrease.

In case the girl run to the right, the boy would move in the second quadrant, the angle θ would increase as the boy approaches the girl.

What is your set-up? Check the signs.

ehild

 

[ehild]

If you expand the numerator, the second term is easy to integrate. The first becomes the integral of a cosecant, which is standard enough that you can look it up. If you're interested in doing it from first principles, multiply top and bottom by sine and convert the sin² in the denominator to 1-cos². You can then factorise that and expand it using partial fractions. Each fraction is readily integrated.

There is a standard substitution when you have to integrate a rational function of sines and cosines. All trigonometric functions can be written in terms of tan(x/2), and then the substitution z=tan(x/2), dx = 2/(1+z²) dz can be used.

\sin(x)= \frac {2\tan(x/2)}{1+\tan^2(x/2)}
\cos(x)= \frac {1-\tan^2(x/2)}{1+\tan^2(x/2)}

\int {\frac{1}{\sin(x)}= \frac {1+\tan^2(x/2)}{2\tan(x/2)}dx}= \int {\frac {1+z^2}{2z}2 \frac{1}{1+z^2}dz}=\int {\frac {1}{z} dz}= \log|tan(x/2)|+Cehild