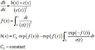JulieK
- 50
- 0
I have the following differential equation
\begin{equation}
\frac{\partial b}{\partial x}=\frac{b-c}{c^{2}}\end{equation}
where b and c are both functions of x. However, although
I have a closed form relation between c and x, I do not have
such a closed form relation between b and x. Is there any analytic
or numeric way to solve this problem. I want a solution linking b,
c and x
\begin{equation}
\frac{\partial b}{\partial x}=\frac{b-c}{c^{2}}\end{equation}
where b and c are both functions of x. However, although
I have a closed form relation between c and x, I do not have
such a closed form relation between b and x. Is there any analytic
or numeric way to solve this problem. I want a solution linking b,
c and x