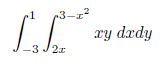Solving Double Integrals: Order of Integration Explained

  • Context: MHB 
  • Thread starter Thread starter Estelle
  • Start date Start date
  • Tags Tags
    Integrals Integration
Click For Summary
SUMMARY

The discussion focuses on solving double integrals by changing the order of integration, specifically addressing the integral $$\int_{-3}^1\int_{2x}^{3-x^2}xy\,dy\,dx$$. Participants emphasize the importance of sketching the region of integration to determine the correct bounds when switching from vertical to horizontal strips. This method is crucial for accurately computing the solution to the integral. The conversation is rooted in concepts typically encountered in a third-semester elementary calculus course.

PREREQUISITES
  • Understanding of double integrals in calculus
  • Familiarity with changing the order of integration
  • Ability to sketch regions of integration
  • Knowledge of evaluating integrals involving polynomial functions
NEXT STEPS
  • Study techniques for sketching regions of integration in double integrals
  • Learn about the properties of double integrals in calculus
  • Explore examples of changing the order of integration with various functions
  • Practice solving double integrals using both vertical and horizontal strips
USEFUL FOR

Students in calculus courses, educators teaching integration techniques, and anyone looking to deepen their understanding of double integrals and their applications.

Estelle
Messages
1
Reaction score
0
Hey guys,

need your help and hope someone takes the time:

I need to solve the double integral by changing the order of Integration.

View attachment 4966

I would really appreciate if you could illustrate the way of how to compute the solution.

Best
Estelle :)
 

Attachments

  • math.JPG
    math.JPG
    1.9 KB · Views: 105
Physics news on Phys.org
Hello and welcome to MHB, Estelle! :D

I have moved this thread, since it is a problem more likely found in the 3rd semester of an elementary calculus course.

Are you certain the problem isn't actually:

$$\int_{-3}^1\int_{2x}^{3-x^2}xy\,dy\,dx$$?
 
Assuming that what Mark has posted is correct, to reverse the order of integration you need to SKETCH the region of integration, and then figure out your bounds by using horizontal strips instead of vertical ones...
 

Similar threads

High School Explain Integration to me, please
  • · Replies 5 ·
Replies
5
Views
3K
Undergrad Solving an Integral using Feyman's trick
  • · Replies 8 ·
Replies
8
Views
2K
Undergrad Double integrals (line vs. Area)
  • · Replies 3 ·
Replies
3
Views
2K
High School Confused about holding variables constant during integration
  • · Replies 15 ·
Replies
15
Views
4K
MHB How do I set up double integrals for different orders of integration?
  • · Replies 4 ·
Replies
4
Views
2K
MHB How Do You Set Up Double Integrals for Different Orders of Integration?
  • · Replies 5 ·
Replies
5
Views
2K
Undergrad Calculating the change of the volume of a sphere using this integral
  • · Replies 3 ·
Replies
3
Views
3K
Undergrad How to evaluate the enclosed area of this implicit curve?
  • · Replies 2 ·
Replies
2
Views
3K
Graduate Integral of 2 Bessel functions of different orders
  • · Replies 3 ·
Replies
3
Views
2K
Graduate Solving an Integral involving a probability density function
  • · Replies 16 ·
Replies
16
Views
2K