lunia
- 5
- 0
Task
Use the Bisection, Newton, and Secant methods to solve (to at least 8
signicant figures) the equation
over the interval [0, 2.5], in radiant units. For the Newton method, try with
several different initial guesses including x0 = 1. With the Secant method,
use the same initial values as for the Bisection, as well as other appropriate
values. Comment on the results by comparing the effectiveness of
each method for this problem. In particular, compare the number of iterations
required by each method to find the solution to a specied accuracy
(at least|f(xroot)| ≤ 10−6
), and see if the behavior you observe tallies with
theoretical predictions where they have been given, in particular the order of
convergence. Provide a careful explanation on your observations.
Hint
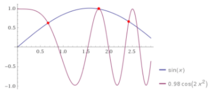
Draw a graph of the equation to understand the behaviors of the equation,
such as the number of solutions and the locations of the roots.
p/s: basically i don't even know what this question want exactly, i do try my best to understand it but i cant. I am sorry
Use the Bisection, Newton, and Secant methods to solve (to at least 8
signicant figures) the equation
sin(x) = 0.98 cos(2x2)over the interval [0, 2.5], in radiant units. For the Newton method, try with
several different initial guesses including x0 = 1. With the Secant method,
use the same initial values as for the Bisection, as well as other appropriate
values. Comment on the results by comparing the effectiveness of
each method for this problem. In particular, compare the number of iterations
required by each method to find the solution to a specied accuracy
(at least|f(xroot)| ≤ 10−6
), and see if the behavior you observe tallies with
theoretical predictions where they have been given, in particular the order of
convergence. Provide a careful explanation on your observations.
Hint
Draw a graph of the equation to understand the behaviors of the equation,
such as the number of solutions and the locations of the roots.
p/s: basically i don't even know what this question want exactly, i do try my best to understand it but i cant. I am sorry