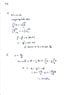SUMMARY
The discussion focuses on solving a physics problem involving a car's braking scenario, specifically calculating the initial speed and stopping time given a deceleration of 10 ft/s² and a stopping distance of 300 ft. The relevant equations used are the SUVAT formulas: v² - v₀² = 2as and v - v₀ = at. The solution confirms that the numerical answers derived from these equations are correct, emphasizing the appropriateness of using standard formulas over integration in this context.
PREREQUISITES
- Understanding of kinematics, specifically SUVAT equations.
- Familiarity with concepts of acceleration and deceleration.
- Basic algebra skills for solving equations.
- Knowledge of units of measurement, particularly feet and seconds.
NEXT STEPS
- Review the derivation and application of SUVAT equations in various scenarios.
- Explore real-world applications of kinematics in automotive safety and design.
- Learn about the effects of different deceleration rates on stopping distances.
- Investigate the role of friction in braking performance and stopping time.
USEFUL FOR
Students studying physics, automotive engineers, and anyone interested in understanding the dynamics of vehicle braking and stopping distances.