Combinatorics
- 31
- 5
- Homework Statement
- A point mass "2m" is rotating around a fixed axis and collides with a stationary mass "m" that starts rotating around another fixed axis. $$\omega$$ is the angular velocity of mass $$2m$$ before the collision and $$0.8\omega$$ is its velocity after the collision.
I need to calculate the energy lost during the collision.
- Relevant Equations
- J=mvr
J initial = J final?
E_k = 0.5mv^2
Unfortunately, I couldn't arrive to the correct answer ($$=0.28mL^2 \omega^2$$ ) and will be happy to understand what am I doing wrong.
**My attempt:**
Using $$
E_k = \frac{1}{2} I \omega^2
$$
I obtain that the difference I need to calculate is
$$
\frac{1}{2} (2mL^2)(0.8\omega)^2 + \frac{1}{2} \left( m \frac{1}{2}^2 L^2 \right) \omega_2 ^2 - \frac{1}{2} (2mL^2) \omega^2,
$$
where $$\omega_2$$ is the angular velocity of mass $$m$$ after the collision. To calculate its velocity, I use conservation of angular momentum and the formula $$J=mvr$$ for a point mass rotating around a fixed axis:
$$
J_i = -2m\omega L^2 = J_f = -2m 0.8 \omega L^2 + m\omega_2 \frac{1}{2}L^2 \Leftrightarrow \omega_2 = -\frac{36}{5}\omega.
$$
And therefore the difference is $$6.12mL^2 \omega^2$$.
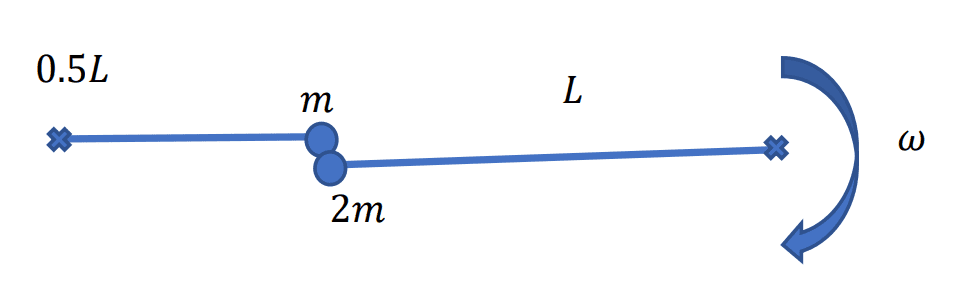
**My attempt:**
Using $$
E_k = \frac{1}{2} I \omega^2
$$
I obtain that the difference I need to calculate is
$$
\frac{1}{2} (2mL^2)(0.8\omega)^2 + \frac{1}{2} \left( m \frac{1}{2}^2 L^2 \right) \omega_2 ^2 - \frac{1}{2} (2mL^2) \omega^2,
$$
where $$\omega_2$$ is the angular velocity of mass $$m$$ after the collision. To calculate its velocity, I use conservation of angular momentum and the formula $$J=mvr$$ for a point mass rotating around a fixed axis:
$$
J_i = -2m\omega L^2 = J_f = -2m 0.8 \omega L^2 + m\omega_2 \frac{1}{2}L^2 \Leftrightarrow \omega_2 = -\frac{36}{5}\omega.
$$
And therefore the difference is $$6.12mL^2 \omega^2$$.
Last edited: