SUMMARY
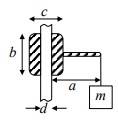
This discussion focuses on solving free-body diagrams for a system involving a mass m on a vertical rod with a nut, sleeve, or bushing that is free to slide. Key points include the identification of forces, moments, and the assumption of static equilibrium. The participants clarify the role of friction and normal forces, leading to the derived expression for the coefficient of friction as μ = 4d/(2a + d), which intriguingly does not depend on mass. The conversation emphasizes the importance of correctly identifying torque moments and the conditions for static equilibrium.
PREREQUISITES
- Understanding of free-body diagrams in mechanics
- Knowledge of static equilibrium principles
- Familiarity with torque and moment calculations
- Basic concepts of friction and normal forces
NEXT STEPS
- Study the principles of static equilibrium in mechanical systems
- Learn about torque calculations and their applications in free-body diagrams
- Explore the relationship between friction coefficients and force ratios
- Investigate the effects of different contact surfaces on friction in mechanical systems
USEFUL FOR
Students and professionals in mechanical engineering, physics, and anyone involved in analyzing forces and motions in mechanical systems, particularly those working with free-body diagrams and static equilibrium.