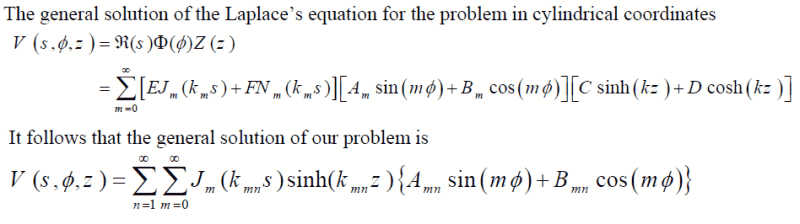SUMMARY
The discussion focuses on solving the Laplace equation in cylindrical coordinates for the potential outside a cylinder with boundary conditions where the potential is zero on the sides and bottom, and V_0 on the top. The key distinction is the use of Bessel functions: Bessel functions of the first kind (Js) are used for the potential inside the cylinder, while Bessel functions of the second kind (Ns) can be employed outside the cylinder due to their finite nature in that region. The general solution is expressed as a double series involving both Js and Ns, with additional boundary conditions ensuring continuity of potential and its derivatives at the cylinder's surface.
PREREQUISITES
- Understanding of Laplace's equation in cylindrical coordinates
- Familiarity with Bessel functions of the first kind (Js) and second kind (Ns)
- Knowledge of boundary value problems in electrostatics
- Basic concepts of potential theory and eigenfunctions
NEXT STEPS
- Study the properties and applications of Bessel functions, particularly in potential theory
- Learn about boundary value problems and their solutions in cylindrical geometries
- Explore the method of separation of variables in solving partial differential equations
- Investigate the implications of singularities in potential functions and their physical interpretations
USEFUL FOR
Physicists, mathematicians, and engineers working on electrostatics, particularly those dealing with cylindrical geometries and boundary value problems in potential theory.