Some algebra in Schutz's textbook

[MathematicalPhysicist]

TL;DR

There's some algebraic manipulation which I need help with on pages 309-313 of Schutz's second edition of "A First Course in GR".

Until I understand how to use maple for my steps by steps algebra manipulation feature (which I learned it has), I'll use PF for some help in the algebra.
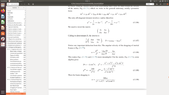
I want to derive the expression for $D=-\Delta \sin^2 \theta$ on page 313 in Equation (11.89).
Attachments of printscreen below.

I wrote two lines, and got discouraged because it seems a long calculation.

$$D=\bigg(\frac{a^2\sin^2 \theta-\Delta^2}{\rho^2}\bigg) \bigg(\frac{(r^2+a^2)^2-a^2\Delta\sin^2\theta}{\rho^2}\bigg)\sin^2\theta-\frac{4a^2M^2 r^2\sin^4\theta}{\rho^4}$$
$$=[a^2\sin^2\theta(r^2+a^2)^2-a^4\Delta \sin^4 \theta-\Delta^2(r^2+a^2)^2+a^2\Delta^3\sin^2\theta]\frac{\sin^2\theta}{\rho^4}-4a^2M^2r^2\sin^4\theta/\rho^4$$
$\Delta$ and $\rho^2$ are given on page 309.

 

[MathematicalPhysicist]

Here are the attachments.

 

[ergospherical]

I remember doing this calculation a short while ago, have a look at roughly half way through post #7 of this thread: https://www.physicsforums.com/threads/finding-the-angular-momentum-of-a-kerr-black-hole.1001913/post-6480105

 

[ergospherical]

I am not sure about your derivation. How did you get the term in the numerator of $(-a^4 \sin^6\theta)$? after you extract $\sin^2(\theta)$ from the numerator you get: $-a^4 \sin^4\theta$ which in the denominator the suitable expression doesn't have a minus sign it has $a^4 \sin^4\theta$. I assume you should be getting: $-\Delta \sin^2\theta (\frac{A}{A})$ where $A$ is some expression that depends on $\theta,r,a$ But you don't get the same expression in the numerator as in the denominator. This is why I wanted maple's to check it for me; but as of yet I don't understand how to use maple to expand this expression while showing all the steps.

There's no mistake! \begin{align*}
K &= -\sin^2{\theta} \left[ \dfrac{\Delta(r^2+a^2)^2 - a^2\sin^2{\theta}(r^2+a^2)^2 - \Delta^2 a^2 \sin^2{\theta} + \Delta a^4 \sin^4{\theta}}{\Sigma^2}\right] \\
&\quad \quad \quad \quad \quad \quad \quad - \, \, \dfrac{a^2\sin^4{\theta}[(r^2+a^2)^2 - 2\Delta(r^2+a^2) + \Delta^2]}{\Sigma^2} \\ \\

&= \dfrac{\Delta \sin^2{\theta}}{\Sigma^2} \left[ 2a^2(r^2+a^2) \sin^2{\theta} - a^4 \sin^4{\theta} - (r^2 +a^2)^2 \right]
\end{align*}Recall that \begin{align*}\Sigma^2 = (r^2+a^2\cos^2{\theta})^2 &= r^4 + 2r^2 a^2(1-\sin^2{\theta}) + a^4 (1-\sin^2{\theta})^2 \\

&= r^4 + 2r^2 a^2 - 2r^2 a^2 \sin^2{\theta} + a^4 -2a^4 \sin^2{\theta} + a^4 \sin^4{\theta} \\

&= -\left[ 2a^2(r^2+a^2) \sin^2{\theta} - a^4 \sin^4{\theta} - (r^2 +a^2)^2 \right]

\end{align*}therefore $K = -\Delta \sin^2{\theta}$

 

[MathematicalPhysicist]

There's no mistake! \begin{align*}
K &= -\sin^2{\theta} \left[ \dfrac{\Delta(r^2+a^2)^2 - a^2\sin^2{\theta}(r^2+a^2)^2 - \Delta^2 a^2 \sin^2{\theta} + \Delta a^4 \sin^4{\theta}}{\Sigma^2}\right] \\
&\quad \quad \quad \quad \quad \quad \quad - \, \, \dfrac{a^2\sin^4{\theta}[(r^2+a^2)^2 - 2\Delta(r^2+a^2) + \Delta^2]}{\Sigma^2} \\ \\

&= \dfrac{\Delta \sin^2{\theta}}{\Sigma^2} \left[ 2a^2(r^2+a^2) \sin^2{\theta} - a^4 \sin^4{\theta} - (r^2 +a^2)^2 \right]
\end{align*}Recall that \begin{align*}\Sigma^2 = (r^2+a^2\cos^2{\theta})^2 &= r^4 + 2r^2 a^2(1-\sin^2{\theta}) + a^4 (1-\sin^2{\theta})^2 \\

&= r^4 + 2r^2 a^2 - 2r^2 a^2 \sin^2{\theta} + a^4 -2a^4 \sin^2{\theta} + a^4 \sin^4{\theta} \\

&= -\left[ 2a^2(r^2+a^2) \sin^2{\theta} - a^4 \sin^4{\theta} - (r^2 +a^2)^2 \right]

\end{align*}therefore $K = -\Delta \sin^2{\theta}$

Yeah, the mistake was on my part...

 

[MathematicalPhysicist]

@ergospherical have you also done the algebra of equation (11.91) on page 314?
The equation is: $(\frac{dr}{d\lambda})^2=g^{rr}[(-g^{tt})E^2+2g^{t\phi}EL-g^{\phi \phi}L^2] \ \ \ (11.91)$.

 

[ergospherical]

Page 314 looks okay to me; which bit's causing you trouble?

 

[MathematicalPhysicist]

Page 314 looks okay to me; which bit's causing you trouble?

How to derive it?
From which Equation or Equations does it follow?
Thanks!

 

[ergospherical]

Firstly, the photon is constrained to the equatorial plane, therefore $p^{\theta} = 0$. Since $g_{\mu \nu} p^{\mu} p^{\nu} = g^{\mu \nu}p_{\mu} p_{\nu} = 0$ it follows that\begin{align*}
g^{tt} p_t p_t + g^{rr} p_r p_r + g^{\phi \phi} p_{\phi} p_{\phi} + 2g^{t\phi} p_t p_{\phi} &= 0 \\
\end{align*}then because $E = -p_t$ and $L=p_{\phi}$ we have\begin{align*}
g_{rr} (p^r)^2 &= -g^{tt} E^2 - g^{\phi \phi} L^2 + 2g^{t\phi}EL \\
(p^r)^2 &= g^{rr} \left[ -g^{tt} E^2 - g^{\phi \phi} L^2 + 2g^{t\phi}EL \right]
\end{align*}since $g^{rr} = 1/g_{rr}$ and $p_r = g_{rr} p^r$. Putting $p^r = dr/d\lambda$ gives 11.91.

 

[MathematicalPhysicist]

@ergospherical sorry to bother you again.

But there's something with equation (11.95) that got me stumped.
How did he get in the numerator the term: $\pm r^2 \Delta^{1/2}$?
I get the following equations:
$\frac{g^{\phi\phi}}{g^{tt}}=\frac{a^2-\Delta}{(r^2+a^2)^2-a^2\Delta}$
So $\omega^2 - \frac{g^{\phi \phi}}{g^{tt}}=\frac{4M^2r^2a^2-(a^2-\Delta)[(r^2+a^2)-a^2\Delta]}{[(r^2+a^2)^2-a^2\Delta]^2}$.
How does the numerator get in the end to: $r^4\Delta$?

I get that the numerator becomes after substituting $-2Mr= \Delta-(r^2+a^2)$:
the numerator: $\Delta^2-2\Delta(r^2+a^2)+(r^2+a^2)^2-a^2(r^2+a^2)^2+\Delta (r^2+a^2)^2 -a^2\Delta^2+a^4 \Delta$.

Now, I am stuck.
How to proceed?, assuming I got until here correctly, which might be wrong... :-D

 

[MathematicalPhysicist]

@ergospherical did you read my post number 10 in this thread?

 

[ergospherical]

I did see it yesterday, I just forgot about it... sorry
You just missed the factor of $a^2$ off of $4M^2 r^2 a^2$. It should be\begin{align*}
((r^2+a^2)^2-a^2\Delta)^2 \left(\omega^2 - \frac{g^{\phi \phi}}{g^{tt}} \right)&=4M^2r^2a^2-(a^2-\Delta)((r^2+a^2)-a^2\Delta) \\

&= a^2 \Delta^2 - 2a^2 \Delta(r^2+a^2) + a^2(r^2 + a^2)^2 \\

&\quad \quad \quad \quad - a^2(r^2 + a^2)^2 + \Delta(r^2 + a^2)^2 + a^4 \Delta - a^2 \Delta ^2 \\ \\

&= \Delta((r^2 + a^2)^2 - 2a^2(r^2 + a^2) + a^4) \\
&= \Delta r^4
\end{align*}

 

[MathematicalPhysicist]

Damn, ****, dang... you are correct!