bhall
- 2
- 1
- TL;DR
- What's the speed of flux? How long does it take to interact with other flux sources?
I have a case where I'm combining a N42 permanent magnet with two coils (20 AWG, 56 turns each, wired in parallel) to create flux transfer. Although model tools such as FEMM or SimScale model a static state of flux interaction, it seems clear based on experimentation that the flux interaction between the steady-state PM and the pulsed coils takes a significant amount of time to interact.
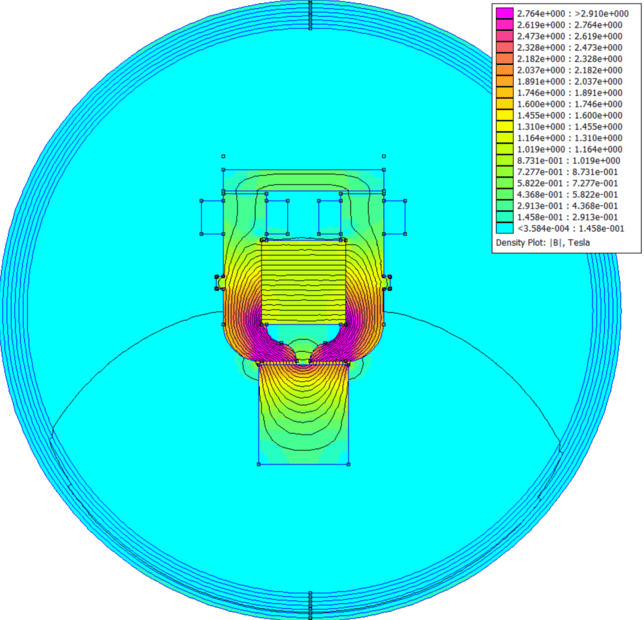
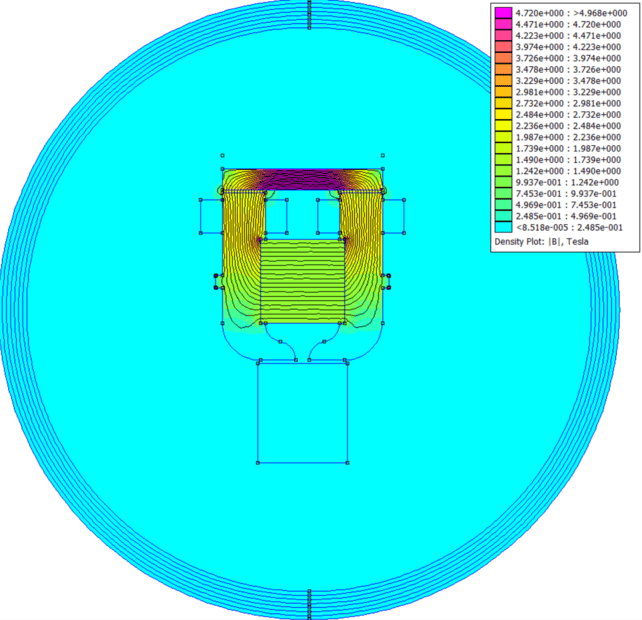
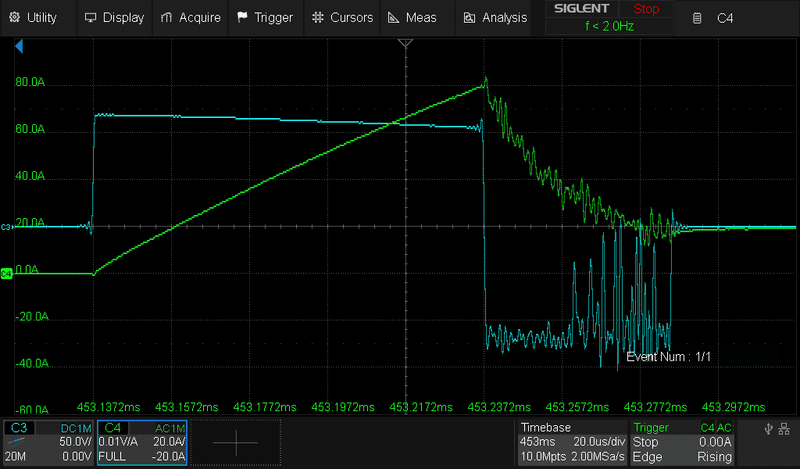
Here I show the models with 30A supplied to the coils in one direction, and then the reverse. As you see it causes the flux to either concentrate in the "back iron" at the top, or mostly at the load at the bottom. But that is steady state. If I instead apply a 10Khz (100uS) pulse that ultimately climbs to 80A before it is cut off, the same effect does not occur. I am currently adding more capacitance to power a longer pulse, but the question becomes - is there a "speed of flux", or the stabilization of the interaction of two sources? If so, how long does it take, and how much amperage is required for a pulse to have the same effect as steady-state? Also, are there any good (and not astronomically priced) software that can help model and answer this question? Or am I missing some important concept here?
Bryan
Here I show the models with 30A supplied to the coils in one direction, and then the reverse. As you see it causes the flux to either concentrate in the "back iron" at the top, or mostly at the load at the bottom. But that is steady state. If I instead apply a 10Khz (100uS) pulse that ultimately climbs to 80A before it is cut off, the same effect does not occur. I am currently adding more capacitance to power a longer pulse, but the question becomes - is there a "speed of flux", or the stabilization of the interaction of two sources? If so, how long does it take, and how much amperage is required for a pulse to have the same effect as steady-state? Also, are there any good (and not astronomically priced) software that can help model and answer this question? Or am I missing some important concept here?
Bryan