Spherical conductor shell problem

[Granger]

Homework Statement

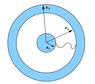
Consider a spherical conducting shell with inner radius R2 and outer radius R3, that has other spherical conductor inside it with radius R1 (this one is solid). Initially the 2 spheres are connected by a wire. We put a positive charge Q on the sphere and after some time we remove the wire that connected the 2 spheres.

What is the charge distribution of charge on the 2 spheres after we remove the potential? If we have charged the inner sphere instead, would the result be different?

Homework Equations

Gauss's law
Electric field is the negative gradient of electrical potential

The Attempt at a Solution

The answer provided was that the charge would all flow to the outer surface of the spherical shell, and the same would happen if we had placed Q on the inside of the conductor shell.

Now I'm trying to find an explanation to this.

At first I thought that because the electric field between R2 and R3 needs to be zero by Gauss law (we are inside a conductor), then the interior charge needs to be zero. Because of that all the charge will flow to the outside. But I don't think that makes sense because we could still have charge outside the inner sphere and on the inside surface of the shell if those charges would be on equilibrium...
Can someone please clarify me about this?
Also I don't understand what would happen if we didn't add charge Q to our system, would the result be different if we didn't add it?

Thanks!

 

[kuruman]

What is the electric potential at r < R3 just before the wire is disconnected?

 

[haruspex]

we could still have charge outside the inner sphere and on the inside surface of the shell if those charges would be on equilibrium.

But could they be? Would the potential be uniform throughout?

 

[Granger]

What is the electric potential at r < R3 just before the wire is disconnected?

Just before the wire is disconnected I don't know the exactly potential (can I know?) but I know that the difference of potential will be zero.

But could they be? Would the potential be uniform throughout?

Oh! They can't be the same because since the radii of the spheres are not the same the potential will never be the same if the charges are equal.

 

[haruspex]

Oh! They can't be the same because since the radii of the spheres are not the same the potential will never be the same if the charges are equal.

That's not quite what I had in mind. If there is a uniform charge on the outer surface of the sphere, what can you say about the potential that generates within the sphere? If you add a uniform charge over a smaller sphere inside it, what can you say about the potential that generates between the spheres?

 

[Granger]

That's not quite what I had in mind. If there is a uniform charge on the outer surface of the sphere, what can you say about the potential that generates within the sphere? If you add a uniform charge over a smaller sphere inside it, what can you say about the potential that generates between the spheres?

So what I said in incorrect?
I'm not quite sure about how to answer your questions, sorry. There is a potential created because of the charge of course, which will cause a difference of potential that will move the charge... But how can I quantify it or how can I know its direction...

 

[haruspex]

So what I said in incorrect?
I'm not quite sure about how to answer your questions, sorry. There is a potential created because of the charge of course, which will cause a difference of potential that will move the charge... But how can I quantify it or how can I know its direction...

If a spherical shell has a uniform charge, is the potential that creates inside it uniform or non-uniform?
Is the potential it creates outside itself uniform or non-uniform?
In the space between two such shells is the total potential uniform or non-uniform?
Is the charge distribution on a conductor stable if the potential varies inside its body?

 

[Granger]

If a spherical shell has a uniform charge, is the potential that creates inside it uniform or non-uniform?
Is the potential it creates outside itself uniform or non-uniform?
In the space between two such shells is the total potential uniform or non-uniform?
Is the charge distribution on a conductor stable if the potential varies inside its body?

Since potential need to be a continuous function. Between the shells it's uniform equal to $$\frac{kQ}{R_3}$$ since electric field is zero. Than outside it should be $$\frac{kQ}{r}$$ r varying. If the potential varies we will have an electric field and because of that charge would be moving. But now how do I connect this to the answer.

 

[haruspex]

Since potential need to be a continuous function. Between the shells it's uniform equal to $$\frac{kQ}{R_3}$$ since electric field is zero. Than outside it should be $$\frac{kQ}{r}$$ r varying. If the potential varies we will have an electric field and because of that charge would be moving. But now how do I connect this to the answer.

Not sure that you have answered my questions. Please answer each in turn.

 

[Granger]

If a spherical shell has a uniform charge, is the potential that creates inside it uniform or non-uniform?

Uniform (it doesn't depend on the distance)

Is the potential it creates outside itself uniform or non-uniform?

Non uniform (it does depend on the distance).

In the space between two such shells is the total potential uniform or non-uniform?

Uniform (constant, not depending on the distance).

Is the charge distribution on a conductor stable if the potential varies inside its body?

It isn't (it creates an electrical field).

 

[haruspex]

Uniform (constant, not depending on the distance).

How can the sum of the non-uniform potential from the inner shell and the uniform potential from the outer shell be uniform?

 

[Granger]

How can the sum of the non-uniform potential from the inner shell and the uniform potential from the outer shell be uniform?

Oh so the outer potential needs also to be uniform?

 

[haruspex]

Oh so the outer potential needs also to be uniform?

I'm not sure what you mean by that.
If you have two concentric shells, each uniformly charged (but not necessarily with the same charge or charge density) then in the space between the shells:
- the potential generated by the outer shell is uniform
- the potential generated by the inner shell is non-uniform
- therefore the total potential there, the sum ofthe two potentials, in non-uniform.
It follows that if the two shells are connected by a conductor the charge distribution is unstable. Stability can only return when there is no charge on the inner shell.

 

[Granger]

When you say"connected by a conductor" you don't mean wire right? Because when they are connected by a wire the difference of potential is zero right?

Also I think I misunderstood before what you meant with inner shell and outer shell.
By inner shell did you meant the space between the sphere and circular shell (white on the following draw) and by outside shell you meant the outside of the conductors?

 

[haruspex]

When you say"connected by a conductor" you don't mean wire right? Because when they are connected by a wire the difference of potential is zero right?

Also I think I misunderstood before what you meant with inner shell and outer shell.
By inner shell did you meant the space between the sphere and circular shell (white on the following draw) and by outside shell you meant the outside of the conductors?

Maybe I misunderstand your puzzlement. You asked

we could still have charge outside the inner sphere and on the inside surface of the shell if those charges would be on equilibrium

Are you referring to the inner and outer surfaces of a thick shell, to the two spheres connected by a wire as at the start of the question, or to two spherical shells not connected at all?
In the last case, yes, there could be a charge on the outer surface of each shell, and the potential in the space between would not be uniform. But in this question the two are connected by a wire initially. Is there any way charge could flow when the wire is cut?

 

[haruspex]

By the way, I assume this is a typo, and it should read "after we remove the wire"

after we remove the potential?

 

[Granger]

Yes it was a typo I meant wire.

I'm really confused right now so let me rephrase my question.
I understand and it makes sense to me that all the charge is on the outer surface of the shell.
My 2 questions were:
- why is it not possible that we have for example (I will call totq the total charge in a surface): -totq in the inner side of the shell; +totq in the surface of the solid sphere. Is it because of the non-uniform potential that would be created?
- I also asked about the influence of the charge placed on the system (in the 1st case in the outer surface of the shell and in the 2nd case on the surface of the solid sphere). If that charge was not there, would charge flow after we remove the wire?

 

[haruspex]

why is it not possible that we have for example (I will call totq the total charge in a surface): -totq in the inner side of the shell; +totq in the surface of the solid sphere.

For each of the two conducting shells, all of its charge must be on the outer surface, for the reasons I gave in post #13.
If the two shells are electrically isolated from each other then, yes, they could be charged in the way you say. The potential in the space between them would not be uniform. But in the question in this thread, they are initially connected by a wire, so at that time all the charge will be on the outer surface of the outer shell.

If that charge was not there, would charge flow after we remove the wire?

I fail to see how removing the wire could result in any charge flow. Everything was already stable.

 

[Granger]

For each of the two conducting shells, all of its charge must be on the outer surface, for the reasons I gave in post #13.
If the two shells are electrically isolated from each other then, yes, they could be charged in the way you say. The potential in the space between them would not be uniform. But in the question in this thread, they are initially connected by a wire, so at that time all the charge will be on the outer surface of the outer shell.

I fail to see how removing the wire could result in any charge flow. Everything was already stable.

I keep getting more confused I'm sorry.
So charge flows to the outside because they are connected initially by the wire?? Why? Shouldn't the solid conducting sphere have the same potential as the inner surface of the outer shell? Why does that potential need to be zero? Is it because of the fact that if it wasn't zero than no charge. But the solution says that the charge flows to the outside after we remove the wire...

 

[haruspex]

Shouldn't the solid conducting sphere have the same potential as the inner surface of the outer shell?

You are confusing the net potential of that sphere with the potential due only to its own charge.
The charge on the outer shell generates a potential everywhere inside itself. To get the net potential you must add any from the solid sphere. With all charge having left th solid sphere, that adds nothing, so everywhere inside the shell has the same potential.