binbagsss
- 1,291
- 12
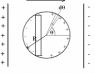
See image attached.
(I've had a google but can't find anything).
I am trying to understand the expression : Rdθ.2∏Rsinθ
Here are my thoughts so far:
Rdθ is the width of a strip, θ being the variable changing/to integrate over, giving arise to the elements.
2∏Rsinθ must then be the length. However I don't understand this expression.
I think I understand Rdθ - it is the arc length.
Here are my length thoughts: From the triangle sin θ =(l/2)/R, where l is the length we are after, and l/2, because this triangle only gives half of the length we are after.
Ofc this must be wrong, as I have a ∏ unexplained.
Many thanks to anyone who can help shed some light on this, greatly appreciated !
(I've had a google but can't find anything).
I am trying to understand the expression : Rdθ.2∏Rsinθ
Here are my thoughts so far:
Rdθ is the width of a strip, θ being the variable changing/to integrate over, giving arise to the elements.
2∏Rsinθ must then be the length. However I don't understand this expression.
I think I understand Rdθ - it is the arc length.
Here are my length thoughts: From the triangle sin θ =(l/2)/R, where l is the length we are after, and l/2, because this triangle only gives half of the length we are after.
Ofc this must be wrong, as I have a ∏ unexplained.
Many thanks to anyone who can help shed some light on this, greatly appreciated !